Unit 04 - Essential problems

Parametric curves

01

Convert parametric curve to function graph

Write the following curves as the graphs of a function . (Find for each case.)

(a) , and

(b) , and

Sketch each curve.

Link to original

05

Convert function graph to parametric curve

Find parametric curves whose images are the following graphs:

(a) and

(b) and

Link to original

06

Parametric concavity

Find the intervals of on which the parametric curve is concave up.

Link to original

09

Cycloid - Arclength and surface area of revolution

Consider the cycloid given parametrically by .

(a) Find the length of one arch of the cycloid.

(b) Suppose one arch of the cycloid is revolved around the -axis. Find the area of this surface of revolution.

Link to original

Polar curves

01

Convert points: Cartesian to Polar

Convert the Cartesian (rectangular) coordinates for these points into polar coordinates:

(a) (b) (c) (d)

Link to original

03

Polar curve - Vertical or horizontal tangent lines

Find all points on the given curve where the tangent line is horizontal or vertical.

Hint: First determine parametric Cartesian coordinate functions using as the parameter.

Link to original

06

Convert equations: Cartesian to Polar

Convert the Cartesian equation to a polar equation. Be sure to simplify.

(a) (b) (c)

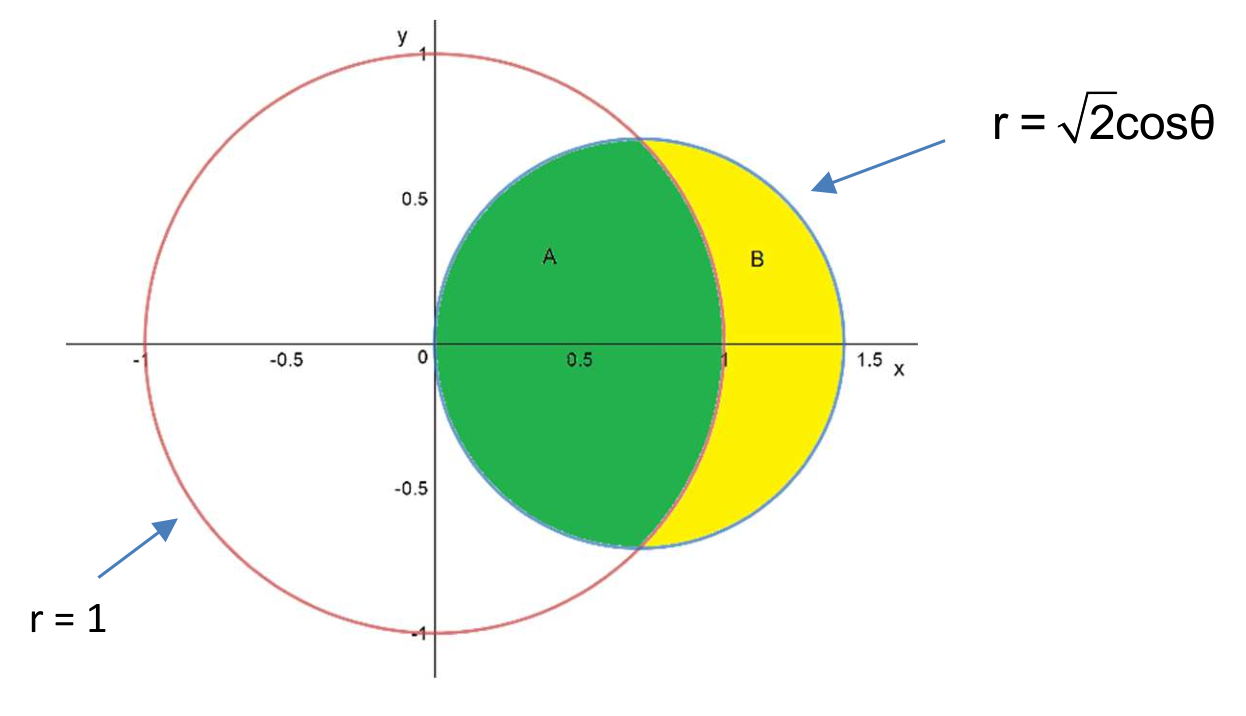
Link to original

10

Polar coordinates - lunar areas

(a) Find the area of the green region.

(b) Find the area of the yellow region.

Link to original

12

Area of an inner loop

A limaçon is given as the graph of the polar curve .

Find the area of the inner loop of this limaçon.

Link to original

Complex numbers

03

Complex forms - exponential to Cartesian

Write each number in the form .

(a) (b)

Link to original

09

Complex products and quotients using polar

For each pair of complex numbers and , compute:

(a)

(b)

(Use polar forms with .)

Link to original

10

Complex powers using polar

Using De Moivre’s Theorem, write each number in the form .

(a) (b)

(First convert to polar/exponential, then compute the power, then convert back.)

Link to original

11

Complex roots using polar

Find each of the indicated roots.

(a) The four roots of .

(b) The three cube () roots of .

Try to write your answer in form if that is not hard, otherwise leave it in polar form.

Link to original