Stepwise problems - Thu. 11:59pm
Moments and CoM
01
01
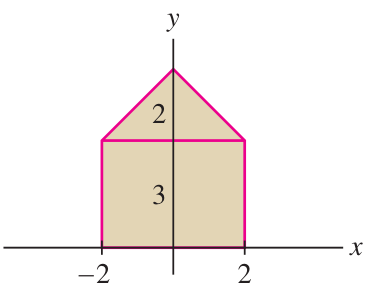
Center of mass of a house
A “house” is the region bounded by the (non-regular) pentagon with vertex points at
, , , , . Find the CoM of the house using additivity of moments.
Link to originalSolution
01
(1) Compute masses:
(2) Consider symmetries of rectangle:
Therefore
and: Therefore:
(3) Consider symmetry of triangle:
(4) Compute
by integration:
(5) Optional step: infer
:
(6) Additivity of moments:
(7) Compute CoM:
Thus:
Link to original
02
02
CoM of region between curves
Find the CoM of the region between the graph of
and the graph of over . Link to originalSolution
02
Option 1: In terms of
. (1) Mass of region:
(2) Integral formula for
:
(3) Integral formula for
:
(4) Compute
:
Option 2: In terms of
. (1) Mass:
(2)
:
(3)
: Link to original
Improper integrals
03
01
Comparison test
Use the comparison test to determine whether the integral converges:
Solution
03
(1) Find comparable integrand:
Higher power dominates for large
: Therefore, compare to
.
(2) Make comparison:
And:
because it is a
-integral with . By the Comparison Test, we conclude that:
Link to original
Regular problems - Sun. 11:59pm
Moments and CoM
04
03
FlatCoMMan
Find the center of mass of FlatCoMMan. Assume a constant mass density
. Use additivity of moments.
Link to originalSolution
04
Assume
for all of these. The value of
does not affect the CoM point if is a constant. Region 1:
Region 2:
Region 3:
Region 4:
Region 5:
Region 6:
Region 7:
FlatCoMMan:
Link to original
05
04
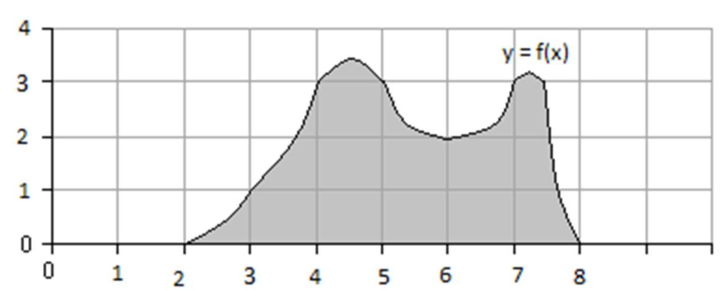
CoM from Simpson’s
Use Simpson’s rule (with 6 subintervals) to estimate the centroid of this region:
You will need to estimate
and and with three separate integrals. You can use a calculator for your arithmetic. Link to originalSolution
05
(1) Simpson’s Rule formula:
(2) Simpson’s for total mass
: Therefore:
So:
(3) Simpson’s for moment to
-axis: Integral formula:
Approximate with
:
(4) Simpson’s for moment to
-axis: Integral formula:
Approximate with
:
(5) Compute CoM:
Link to original
Improper integrals
06
02
Proper vs. improper
For each integral below, determine whether it is proper or improper, and if improper, explain why.
(a)
(b) (c) (d)
(e) (f) Link to originalSolution
06
(a) Improper: integrand
as . Note: this converges too, since it’s a
-integral to zero with . (b) Proper: no source of infinity.
Note: automatically converges.
(c) Improper:
as . Note: this diverges. Antiderivative is
as . (d) Improper: infinite upper bound.
Note: this diverges. Antiderivative is
which has no limit as . (e) Improper: infinite upper bound.
Note: this diverges. Antiderivative is
as . (L’Hopital’s rule, indeterminate form.) (f) Improper: infinite integrand at
. Note: this converges. Antiderivative is
Link to originalas . (Same indeterminate form as (e).)
07
03
Gabriel’s Horn - Volume and surface of revolution
The curve
for is rotated about the -axis. The resulting shape is Gabriel’s Horn. (a) Find the volume enclosed by the horn by evaluating a convergent improper integral.
(b) Show that the surface area of the horn is infinite by applying comparison to a
-integral which is divergent. Link to originalSolution
07
Volume:
Surface area:
But notice this:
But
diverges! So by the comparison test,
Link to originaldiverges as well.
08
04
Computing improper integrals
For each integral below, give the limit interpretation of improper integral and then compute the limit. Based on that result, state whether the integral converges. If it converges, what is its value?
(a)
(b) (c) Link to originalSolution
09
(a)
(1) Definition of improper integral:
(2) Antiderivative and limit:
(b)
(1) Definition of improper integral:
(2) Antiderivative and limit:
(c)
(1) Definition of improper integral:
(2) Antiderivative and limit:
Link to original
09
05
Computing improper integrals
For each integral below, give the limit interpretation of improper integral and then compute the limit. Based on that result, state whether the integral converges. If it converges, what is its value?
(a)
(b) (c) Link to originalSolution
10
(a)
(1) Definition of improper integral:
(2) Antiderivative and limit:
Note A: Use L’Hopital:
(b)
(1) Definition of improper integral:
(2) Antiderivative and limit:
(c)
(1) Definition of improper integral:
(2) Antiderivative and limit:
Link to original