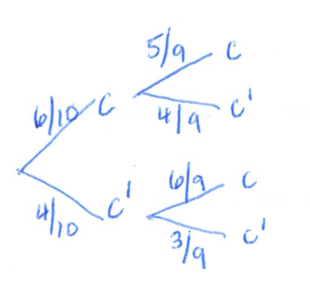01
Bin of marbles
A bin contains 5 red marbles, 7 blue marbles, and 3 white marbles.
We draw a random marble. If it’s red, we put it back, if it’s not red, we keep it. We do this three times.
(a) What is the probability of getting red then white then blue?
(b) Suppose the last draw was blue. What is the probability that the first was red?
Solution
09
(a)
(1) Define events.
We define the sample space as
.
is the first ball drawn, the second, and the third.
represents the event in which a red ball is drawn, represents the event in which a white ball is drawn, represents the event in which a blue ball is drawn.
(2) Compute
.
(b)
(1) We are asked to compute
. Use Bayes’ Theorem to set up formula for .
(2) Find probabilities for all relevant combinations.
(3) Plug in values.
Link to original
02
Homework part errors
A homework problem has 10 different parts. You submit and are told that 4 of the 10 answers you provided are incorrect, but you are not told which parts are incorrect.
(a) What is the probability you will have gotten the first part correct and the second part incorrect? Draw a tree diagram.
(b) Suppose the 4 errors have occurred in the first 6 parts. In this case, how many possible arrangements are there for these 4 errors?
(c) What is the probability the 4 errors occurred in the first 6 parts?
Solution
18
(a)
Note:
gives the wrong answer! (b)
(c)
Link to original