Bayes’ Theorem
01 Theory
Theory 1
Bayes’ Theorem
For any events
and : Bayes’ Theorem is sometimes called Bayes’ Rule.
Bayes’ Theorem - Derivation
Start with the observation that
, or event “ AND ” equals event “ AND ”. Apply the multiplication rule to each of order:
Equate them and rearrange:
The main application of Bayes’ Theorem is to calculate
when it is easy to calculate from the problem setup. Often this occurs in multi-stage experiments where event describes outcomes of an intermediate stage. Note: these notes use alphabetical order
Link to original, as a mnemonic for temporal or logical order, i.e. that comes first in time, or that otherwise that is the prior conditional from which it is easier to calculate .
02 Illustration
Example - Bayes’ Theorem - COVID tests
Bayes’ Theorem: COVID tests
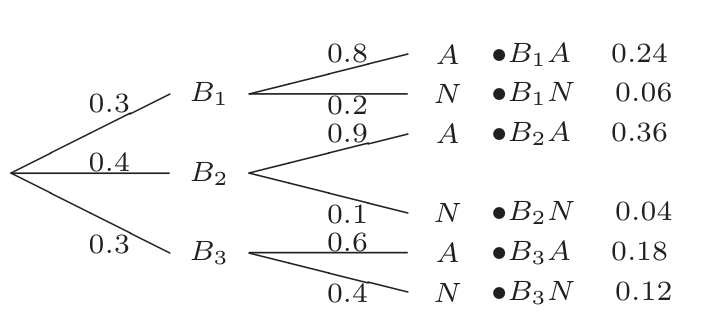
Assume that 0.5% of people have COVID. Suppose a COVID test gives a (true) positive on 96% of patients who have COVID, but gives a (false) positive on 2% of patients who do not have COVID. Bob tests positive. What is the probability that Bob has COVID?
Solution
(1) Label events.
Event
: Bob is actually positive for COVID Event
: Bob is actually negative; note Event
: Bob tests positive Event
: Bob tests negative; note
(2) Identify knowns.
Know:
Know:
Know:
and therefore We seek:
(3)
Translate Bayes’ Theorem.
Using
and in the formula: We know all values on the right except
(4)
Use Division into Cases.
Observe:
Division into Cases yields:
Important to notice this technique!
- It is a common element of Bayes’ Theorem application problems.
- It is frequently needed for the denominator.
Plug in data and compute:
(5) Compute answer.
Plug in and compute:
Intuition - COVID testing
Some people find the low number surprising. In order to repair your intuition, think about it like this: roughly 2.5% of tests are positive, with roughly 2% coming from false positives, and roughly 0.5% from true positives. The true ones make up only
of the positive results! (This rough approximation is by assuming
.) If two tests both come back positive, the odds of COVID are now 98%.
If only people with symptoms are tested, so that, say, 20% of those tested have COVID, that is,
, then one positive test implies a COVID probability of 92%.
Exercise - Bayes’ Theorem and Multiplication: Inferring
Inferring bin from marble
There are marbles in bins in a room:
- Bin 1 holds 7 red and 5 green marbles.
- Bin 2 holds 4 red and 3 green marbles.
Your friend goes in the room, shuts the door, and selects a random bin, then draws a random marble. (Equal odds for each bin, then equal odds for each marble in that bin.) He comes out and shows you a red marble.
What is the probability that this red marble was taken from Bin 1?
Link to original
Independence
03 Theory
Theory 1
Two events are independent when information about one of them does not change our probability estimate for the other. Mathematically, there are three ways to express this fact:
Independence
Events
and are independent when these (logically equivalent) equations hold:
The last equation is symmetric in
and .
- Check:
and - This symmetric version is the preferred definition of the concept.
Link to originalMultiple-independence
A collection of events
is mutually independent when every subcollection satisfies: A potentially weaker condition for a collection
is called pairwise independence, which holds when all 2-member subcollections are independent: One could also define
-member independence, or -member independence. Plain ‘independence’ means any-member independence.
04 Illustration
Exercise - Independence and complements
Independence and complements
Prove that these are logically equivalent statements:
and are independent and are independent and are independent Make sure you demonstrate both directions of each equivalency.
Link to original
Example - Checking independence by hand
Independence by hand: red and green marbles
A bin contains 4 red and 7 green marbles. Two marbles are drawn.
Let
be the event that the first marble is red, and let be the event that the second marble is green. (a) Show that
and are independent if the marbles are drawn with replacement. (b) Show that
and are not independent if the marbles are drawn without replacement. Solution
(a) With replacement.
(1) Identify knowns.
Know:
Know:
(2) Compute both sides of independence relation.
Relation is
Right side is
For
, have ways to get , and total outcomes. So left side is
, which equals the right side. (b) Without replacement.
(1) Identify knowns.
Know:
and therefore We seek:
and
(2) Find
using Division into Cases. Division into cases:
Therefore:
Find these by counting and compute:
(3) Find
using Multiplication rule. Multiplication rule (implicitly used above already):
(4) Compare both sides.
Left side:
Whereas, right side:
But
Link to originalso and they are not independent.
Tree diagrams
05 Theory
Theory 1
A tree diagram depicts the components of a multi-stage experiment. Nodes, or branch points, represent sources of randomness.
An outcome of the experiment is represented by a pathway taken from the root (left-most node) to a leaf (right-most node). The branch chosen at a given node junction represents the outcome of the “sub-experiment” constituting that branch point. So a pathway encodes the outcomes of all sub-experiments.
Each branch from a node is labeled with a probability number. This is the probability that the sub-experiment of that node has the outcome of that branch.
- The probability label on some branch is the conditional probability of that branch, assuming the pathway from root to prior node.
- In the example:
. - Therefore, branch labels from given node sum to 1. (Law of Total Probability)
- The probability of a given (overall) outcome is the product of the probabilities on each branch of the pathway to that outcome.
- Makes sense, because (e.g.):
- More generally: remember that (e.g.):
- This overall outcome probability may be written at the leaf.
One can also use a tree diagram to remember quickly how to calculate certain probabilities.
For example, what is
in the diagram? Answer: add up the pathway probabilities (leaf numbers) terminating in . That makes For example, what is
? Answer: divide the leaf probability of by the total probability of . That makes: Link to original
06 Illustration
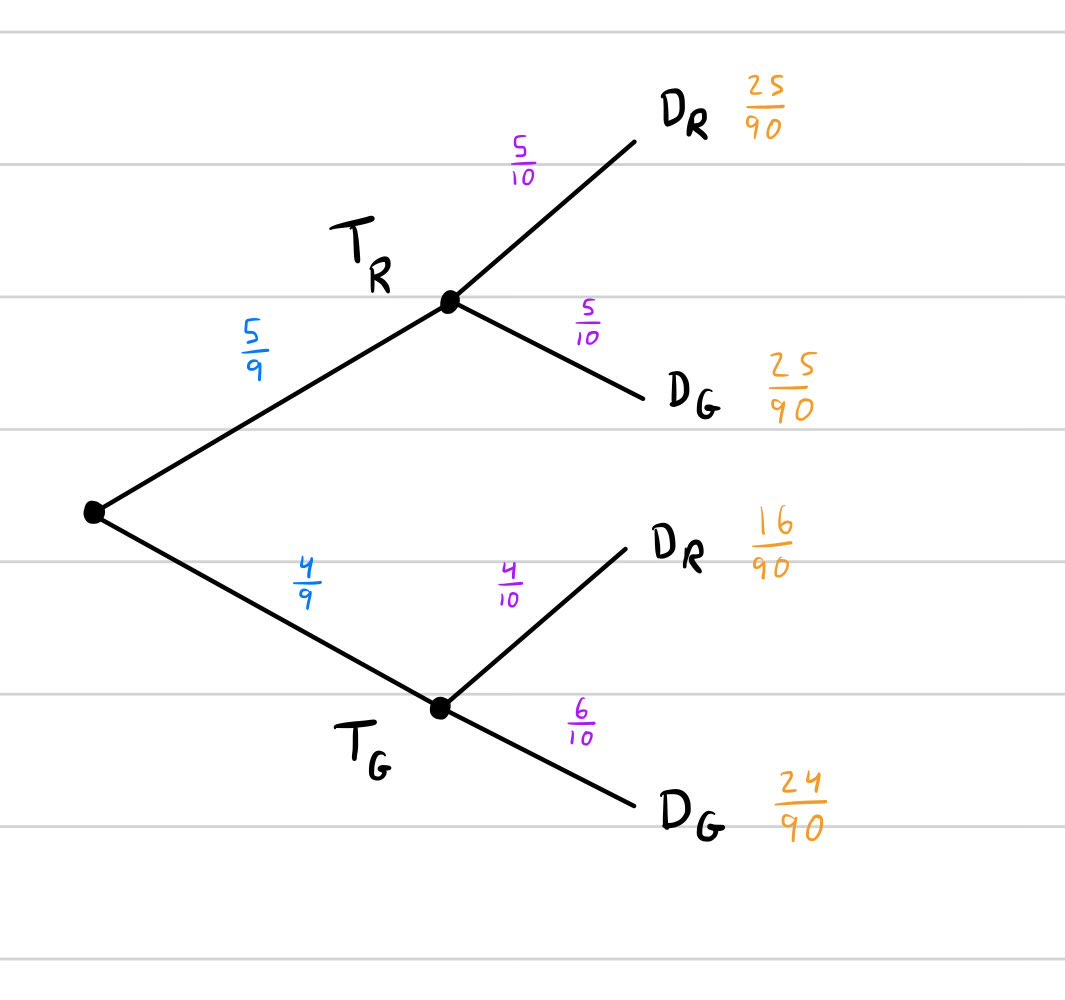
Example - Tree diagrams: Marble transferred, marble drawn
Marble transferred, marble drawn
Setup:
- Bin 1 holds five red and four green marbles.
- Bin 2 holds four red and five green marbles.
Experiment:
- You take a random marble from Bin 1 and put it in Bin 2 and shake Bin 2.
- Then you draw a random marble from Bin 2 and look at it.
Questions:
(a) What is the probability you draw a red marble?
(b) Supposing that you drew a red marble, what is the probability that a red marble was transferred?
Solution
(1) Construct the tree diagram.
Identify sub-experiments, label events, compute probabilities:
(2) For (a), compute
. Add up leaf numbers for
at leaf:
(3) For (b), compute
. Conditional probability:
Plug in data and compute:
Interpretation: mass of desired pathway over mass of possible pathways.
Link to original
Counting
07 Theory
Theory 1
In many “games of chance”, it is assumed by symmetry principles that all outcomes are equally likely. From this assumption we infer the rule for
: In words: the probability of event
is the number of outcomes in divided by the number of possible outcomes. When this formula applies, it is important to be able to count total outcomes, as well as outcomes satisfying various conditions.
Permutations
Permutations count the number of ordered lists one can form from some items. For a list of
items taken from a total collection of , the number of permutations is: To see where this comes from: There are
choices for the first item, then for the second, then … then for the item. So the number is . Observe: Combinations, binomial coefficient
Combinations count the number of sets (ignoring order) one can form from some items. We define a notation for it like this:
This counts the number of sets of
distinct elements taken from a total collection of items. Another name for combinations is the binomial coefficient.
This formula can be derived from the formula for permutations. The possible permutations can be partitioned into combinations: each combination gives a set, and by specifying an ordering of elements in the set, we get a permutation. For a set of
elements taken from items, there are ways to put them into a specific order. So the number of permutations must be a factor of greater than the number of combinations. This notation,
, is also called the binomial coefficient because it provides the coefficients of a binomial expansion: For example:
There are also ‘higher’ combinations:
Multinomial coefficient
The general multinomial coefficient is defined by the formula:
where
and . The multinomial coefficient measures the number of ways to partition
items into sets with sizes , respectively. Notice that
Link to originalso we already defined these values with binomial coefficients. But with , we have new values. They correspond to the coefficients in multinomial expansions. For example gives coefficients for .
08 Illustration
Exercise - Combinations: Counting teams with Cooper
Counting teams with Cooper
A team of 3 student volunteers is formed at random from a class of 40. What is the probability that Cooper is on the team?
Link to original
Example - Combinations: Groups with Haley and Hugo
Haley and Hugo from 2 groups of 3
The class has 40 students. Suppose the professor chooses 3 students Wednesday at random, and again 3 on Friday. What is the probability that Haley is chosen today and Hugo on Friday?
Solution
(1) Count total outcomes.
Have
possible groups chosen Wednesday. Have
possible groups chosen Friday. Therefore
possible groups in total.
(2) Count desired outcomes.
Groups of 3 with Haley are same as groups of 2 taken from others.
Therefore have
groups that contain Haley. Have
groups that contain Hugo. Therefore
total desired outcomes.
(3) Compute probability.
Let
label the desired event. Use formula:
Therefore:
Link to original
Example - Counting VA license plates
Counting VA license plates
A VA license plate has three letters (with no I, O, or Q) followed by four numerals. A random plate is seen on the road.
(a) What is the probability that the numerals are in increasing order?
(b) What is the probability that at least one number is repeated?
Solution
(a)
(1) Count ways to have 4 numerals in increasing order.
Any four distinct numerals have a single order that’s increasing.
There are
ways to choose 4 numerals from 10 options.
(2) Count ways to have 3 letters in order except I, O, Q.
26 total letters, 3 excluded, thus 23 options.
Repetition allowed, thus
possibilities.
(3) Count total plates with increasing numerals.
Multiply the options:
(4) Count total plates.
Have
options for letters. Have
options for numbers. Thus
possible plates.
(5) Compute probability.
Let
label the event that a plate has increasing numerals. Use the formula:
Therefore:
(b)
(1) Count plates with at least one number repeated.
“At least” is hard! Try complement: “no repeats”.
Let
be event that no numbers are repeated. All distinct. Count possibilities:
Total license plates is still
. Therefore, license plates with at least one number repeated:
(2) Compute probability.
Desired outcomes over total outcomes:
Link to original
Counting out 4 teams
Counting out 4 teams
A board game requires 4 teams of players. How many configurations of teams are there out of a total of 17 players if the number of players per team is 4, 4, 4, 5, respectively.
Link to original