Examples - Unit 01

Events and outcomes

01 - Coin flipping

Flip a fair coin two times and record both results.

• Outcomes: sequences, like or .

• Sample space: all possible sequences, i.e. the set .

• Events: for example:

With this setup, we may combine events in various ways to generate other events:

• Complex events: for example:

  • , or in words: Notice that the last one is a complete description, namely the outcome .

  • , or in words:

02 - Coin flipping: counting subsets

Flip a fair coin five times and record the results.

How many elements are in the sample space? (How big is ?) How many events are there? (How big is ?)

Solution

Probability models

03 - Lucia is Host or Player

The professor chooses three students at random for a game in a class of 40, one to be Host, one to be Player, one to be Judge. What is the probability that Lucia is either Host or Player?

Solution

• &&& Set up the probability model.

  • Label the students to . Write for Lucia’s number.

  • Outcomes: assignments such as

    • These are ordered triples with distinct entries in .

  • Sample space: is the collection of all such distinct triples

  • Events: any subset of

  • Probability measure: assume all outcomes are equally likely, so for all

  • In total there are triples of distinct numbers.

  • Therefore for any specific outcome .

  • Therefore for any event . (Recall is the number of outcomes in .)

• && Define the desired event.

  • Want to find

  • Define and . Thus:

  • So we seek .

• &&& Compute the desired probability.

  • Importantly, (mutually exclusive). There are no outcomes in in which Lucia is both Host and Player.

  • By additivity, we infer .

  • Now compute .

    • There are ways to choose and from the students besides Lucia.

    • Therefore .

    • Therefore:

  • Now compute . It is similar: .

  • Finally compute that , so the answer is:

04 - iPhones and iPads

At Mr. Jefferson’s University, 25% of students have an iPhone, 30% have an iPad, and 60% have neither.

What is the probability that a randomly chosen student has some iProduct? (Q1)

What about both? (Q2)

Solution

• &&& Set up the probability model.

  • A student is chosen at random: an outcome is the chosen student.

  • Sample space is the set of all students.

  • Write and concerning the chosen student.

  • All students are equally likely to be chosen: therefore for any event .

  • Therefore and .

  • Furthermore, . This means 60% have “not iPhone AND not iPad”.

• & Define the desired event.

  • Q1:

  • Q2:

• &&& Compute the probabilities.

  • We do not believe and are exclusive.

  • Try: apply inclusion-exclusion:

  • We know and . So this formula, with given data, RELATES Q1 and Q2.

  • Notice the complements in and try Negation.

  • Negation: DOESN’T HELP.

  • Try again: Negation:

  • And De Morgan (or a Venn diagram!):

  • Therefore:

  • We have found Q1: .

  • Applying the RELATION from inclusion-exclusion, we get Q2:

Conditional probability

05 - Simplifying conditionals inclusion

Let . Simplify the following values:

Solution

06 - Coin flipping: at least 2 heads

Flip a fair coin 4 times and record the outcomes as sequences, like .

Let be the event that there are at least two heads, and the event that there is at least one heads.

First let’s calculate .

Define , the event that there were exactly 2 heads, and , the event of exactly 3, and the event of exactly 4. These events are exclusive, so: Each term on the right can be calculated by counting:

Therefore, .

Now suppose we find out that “at least one heads definitely came up”. (Meaning that we know .) For example, our friend is running the experiment and tells us this fact about the outcome.

Now what is our estimate of likelihood of ?

The formula for conditioning gives: Now . (Any outcome with at least two heads automatically has at least one heads.) We already found that . To compute we simply add the probability , which is , to get .

Therefore:

07 - Multiplication: flip a coin, then roll dice

Flip a coin. If the outcome is heads, roll two dice and add the numbers. If the outcome is tails, roll a single die and take that number. What is the probability of getting a tails AND a number at least 3?

Solution This “two-stage” experiment lends itself to a solution using the multiplication rule for conditional probability.

• & Label the events of interest.
  • Let and be the events that the coin showed heads and tails, respectively.
  • Let be the events that the final number is , respectively.
  • The value we seek is .
• & Observe known (conditional) probabilities.
  • We know that and .
  • We know that , for example, or that .
• && Apply “multiplication” rule.
  • This rule gives:
  • We know and can see by counting that .
  • Therefore .

08 - Multiplication: draw two cards

Two cards are drawn from a standard deck (without replacement).

What is the probability that the first is a 3, and the second is a 4?

Solution This “two-stage” experiment lends itself to a solution using the multiplication rule for conditional probability.

• & Label events.
  • Write for the event that the first card is a 3
  • Write for the event that the second card is a 4.
  • We seek .
• & Write down knowns.
  • We know . (It does not depend on the second draw.)
  • Easily find .
    • If the first is a 3, then there are four 4s remaining and 51 cards.
    • So .
• & Apply multiplication rule.
  • Multiplication rule:
  • Therefore

09 - Marble transferred, marble drawn

Setup:

• Bin 1 holds five red and four green marbles.
• Bin 2 holds four red and five green marbles.

Experiment:

• You take a random marble from Bin 1 and put it in Bin 2 and shake Bin 2.
• Then you draw a random marble from Bin 2 and look at it.

What is the probability that the marble you look at is red?

Solution

Bayes’ Theorem

10 - Bayes’ Theorem: COVID tests

Assume that 0.5% of people have COVID. Suppose a COVID test gives a (true) positive on 96% of patients who have COVID, but gives a (false) positive on 2% of patients who do not have COVID. Bob tests positive. What is the probability that Bob has COVID?

Solution

• & Label events.
  • Event : Bob is actually positive for COVID
  • Event : Bob is actually negative; note
  • Event : Bob tests positive
  • Event : Bob tests negative; note
• && Identify knowns.
  • Know:
  • Know:
  • Know: and therefore
  • We seek:
• ! Translate Bayes’ Theorem.
  • Using and in the formula:
  • We know all values on the right except
• !! Use Division into Cases.
  • Observe:
  • Division into Cases yields:
  • !!! Important to notice this technique!
    • It is a common element of Bayes’ Theorem application problems.
    • It is frequently needed for the denominator.
  • Plug in data and compute:
• & Compute answer.
  • Plug in and compute:

11 - Inferring bin from marble

There are marbles in bins in a room:

• Bin 1 holds 7 red and 5 green marbles.
• Bin 2 holds 4 red and 3 green marbles.

Your friend goes in the room, shuts the door, and selects a random bin, then draws a random marble. (Equal odds for each bin, then equal odds for each marble in that bin.) He comes out and shows you a red marble.

What is the probability that this red marble was taken from Bin 1?

Solution

Independence

12 - Independence and complements

Prove that these are logically equivalent statements:

• and are independent
• and are independent
• and are independent

Make sure you demonstrate both directions of each equivalency.

Solution

13 - Independence by hand: red and green marbles

A bin contains 4 red and 7 green marbles. Two marbles are drawn.

Let be the event that the first marble is red, and let be the event that the second marble is green.

• (a) Show that and are independent if the marbles are drawn with replacement.
• (b) Show that and are not independent if the marbles are drawn without replacement.

Solution (a) With replacement.

• & Identify knowns.
  • Know:
  • Know:
• & Compute both sides of independence relation.
  • Relation is
  • Right side is
  • For , have ways to get , and total outcomes.
  • So left side is , which equals the right side.

(b) Without replacement.

• & Identify knowns.
  • Know: and therefore
  • We seek: and
• && Find using Division into Cases.
  • Division into cases:
  • Therefore:
  • Find these by counting and compute:
• & Find using Multiplication rule.
  • Multiplication rule (implicitly used above already):
• & Compare both sides.
  • Left side:
  • Whereas, right side:
  • But so and they are not independent.

Tree diagrams

14 - Marble transferred, marble drawn

Setup:

• Bin 1 holds five red and four green marbles.
• Bin 2 holds four red and five green marbles.

Experiment:

• You take a random marble from Bin 1 and put it in Bin 2 and shake Bin 2.
• Then you draw a random marble from Bin 2 and look at it.

Questions:

• (a) What is the probability you draw a red marble?
• (b) Supposing that you drew a red marble, what is the probability that a red marble was transferred?

Solution

• &&& Construct the tree diagram.
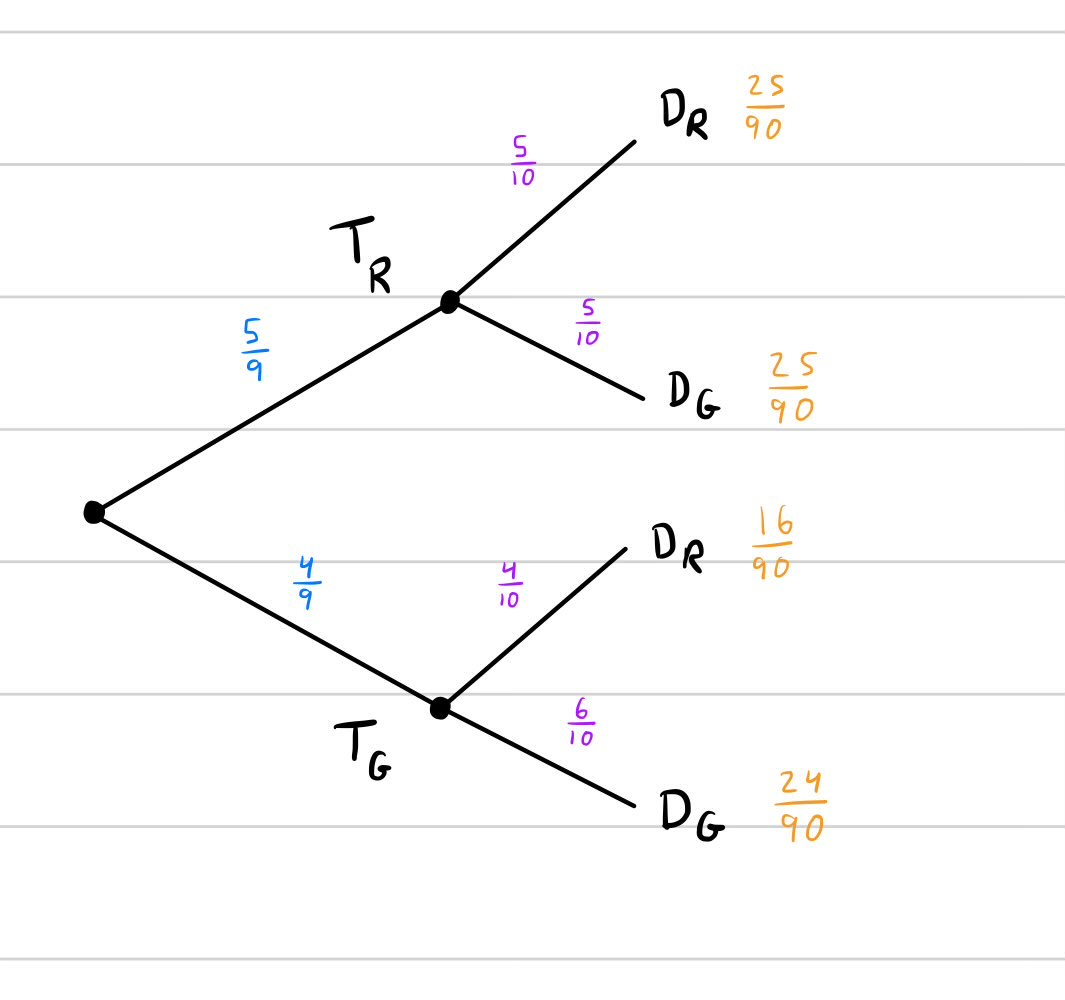
  • Identify sub-experiments, label events, compute probabilities:
• & For (a), compute .
  • Add up leaf numbers for at leaf:
• & For (b), compute .
  • Conditional probability:
  • Plug in data and compute:
  • Interpretation: mass of desired pathway over mass of possible pathways.

Counting

15 - Counting teams with Cooper

A team of 3 student volunteers is formed at random from a class of 40. What is the probability that Cooper is on the team?

Solution

16 - Haley and Hugo from 2 groups of 3

The class has 40 students. Suppose the professor chooses 3 students Wednesday at random, and again 3 on Friday. What is the probability that Haley is chosen today and Hugo on Friday?

Solution

• & Count total outcomes.
  • Have possible groups chosen Wednesday.
  • Have possible groups chosen Friday.
  • Therefore possible groups in total.
• && Count desired outcomes.
  • Groups of 3 with Haley are same as groups of 2 taken from others.
  • Therefore have groups that contain Haley.
  • Have groups that contain Hugo.
  • Therefore total desired outcomes.
• && Compute probability.
  • Let label the desired event.
  • Use formula:
  • Therefore:

17 - Counting VA license plates

A VA license plate has three letters (with no I, O, or Q) followed by four numerals. A random plate is seen on the road.

• (a) What is the probability that the numerals are in increasing order?
• (b) What is the probability that at least one number is repeated?

Solution (a)

• & Count ways to have 4 numerals in increasing order.
  • Any four distinct numerals have a single order that’s increasing.
  • There are ways to choose 4 numerals from 10 options.
• & Count ways to have 3 letters in order except I, O, Q.
  • 26 total letters, 3 excluded, thus 23 options.
  • Repetition allowed, thus possibilities.
• & Count total plates with increasing numerals.
  • Multiply the options:
• & Count total plates.
  • Have options for letters.
  • Have options for numbers.
  • Thus possible plates.
• & Compute probability.
  • Let label the event that a plate has increasing numerals.
  • Use the formula:
  • Therefore:

(b)

• && Count plates with at least one number repeated.
  • ! “At least” is hard! Try complement: “no repeats”.
  • Let be event that no numbers are repeated. All distinct.
  • Count possibilities:
  • Total license plates is still .
  • Therefore, license plates with at least one number repeated:
• & Compute probability.
  • Desired outcomes over total outcomes:

18 - Counting out 4 teams

A board game requires 4 teams of players. How many configurations of teams are there out of a total of 17 players if the number of players per team is 4, 4, 4, 5, respectively.

Solutions