04
(1) We have that
(2) Let
Now, since
(3) Plugging in
06
(a)
(1) Suppose
(2) For the first condition, we have:
and thus the first condition holds for any
(3) For the second condition, by independence, we must have
(4) Thus,
(b)
(1) Define
The mean is
The variance is
Thus,
(2) Note that
(c)
(1) Let
(2) Note that
07
(a)
Marginal PDF of
Then:
(b)
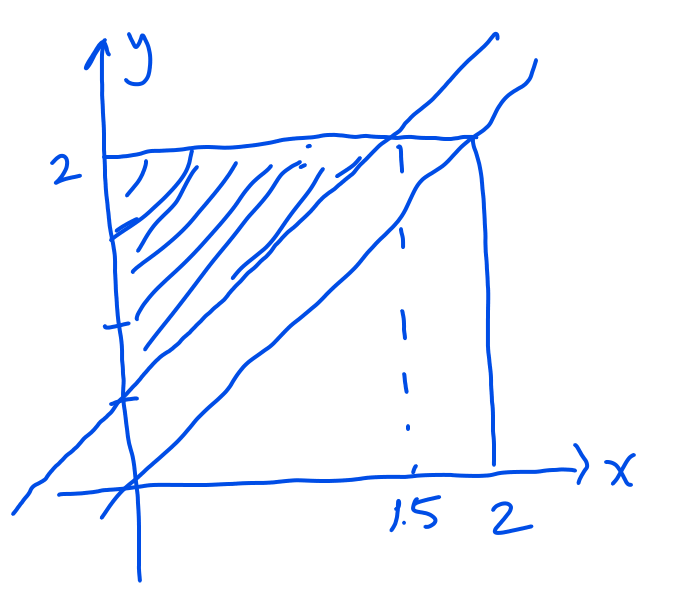
(c)
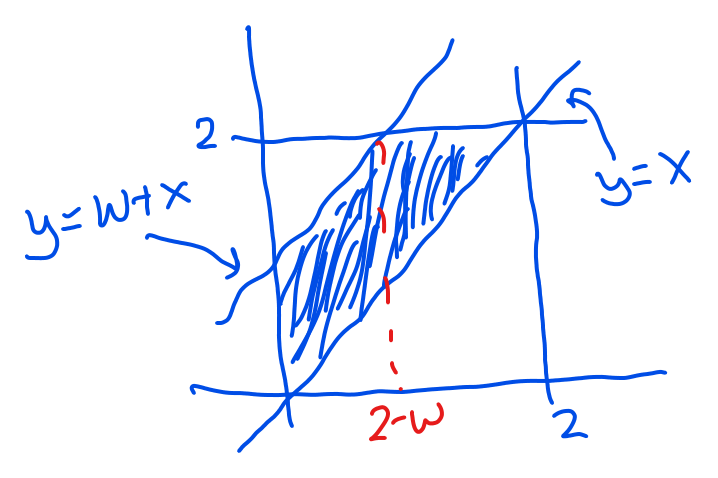
08
(1) PDF of
(2) CDF of
(3) PDF of
09
(a)
Case 1:
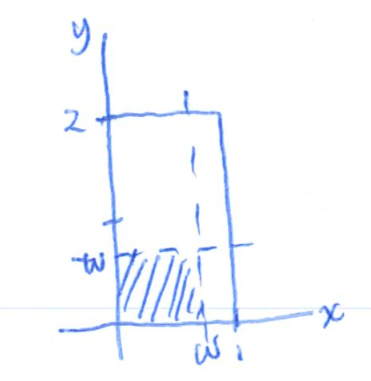
Case 2:
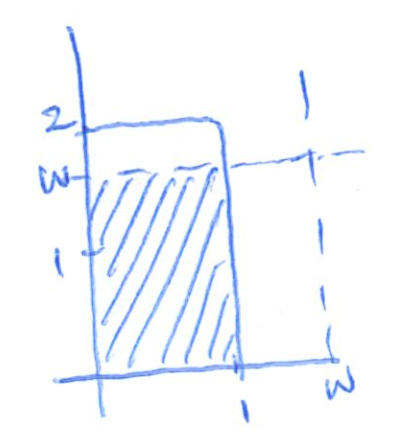
(b)
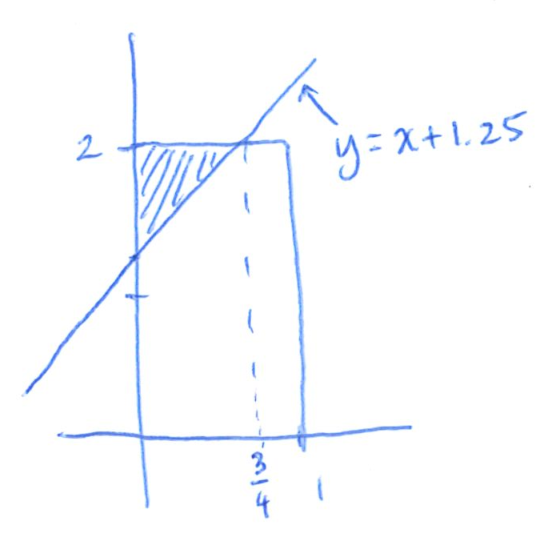
10
11
(a)
Fill the cells using the respective column sum or row sum.
We have , so
: We have , so
: We have , so
: We have , so
(b)
(1) Add up the probabilities in which either
(2) Alternatively, you could use the inclusion-exclusion principle using the marginal sums.
12
| 2 | 3 | |
|---|---|---|
13
(a)
Find the area of the triangle, and find a formula for the PDF.
The area of the triangle is
(b)
(1) Integrate with respect to
(2) Integrate with respect to
(c)
(1) Compute the product
(2) Consider the case wherein
Therefore,
14
(1) Compute the marginal distribution of
(2) Compute the marginal distribution of
(3) Determine independence by multiplying the marginal pdfs.
Since the product of the marginal PDFs equals the joint PDF, we conclude that
(4) Compute the marginal distribution of
(5) Compute the marginal distribution of
(6) Determine independence by multiplying the marginal pdfs.
Therefore,
15
(1) Write the event
(2) Write the terms
(3) Simplify expression for