W10 - HW Solutions

01

(1) Compute :

---

(2) Compute :

---

(3) Compute :

02

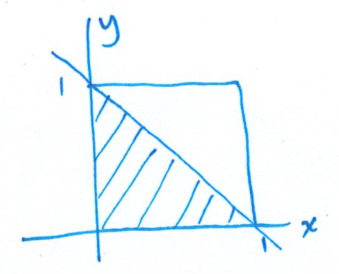
For :

So:

03

(a)

---

(b)

---

(c)

04

(a)

Conditional distribution:

Compute :

Therefore:

---

(b)

Therefore:

05

(a)

Obtain joint from conditional and marginal:

Therefore:

---

(b)

Conditioning the other way:

Marginal distribution of :

Therefore:

06

Find possible combinations of and .

• For a given value of , there are possible options for .
• Thus, in total, there are possible combinations.
• Since , we have that .

(a)

We have that

Thus,

---

(b)

(1) State formula

---

(2) State final answer

---

(c)

Compute expectation:

---

(d)

Find formula for expectation.

07

Integrate joint PDF and solve for .

(a)

Integrate joint PDF with respect to to obtain

---

(b)

Use formula for conditional distribution.

---

(c)

(1) Plug in into the formula found in part (b)

---

(2) Integrate to find expectation.

---

(d)

Integrate formula in part (b) with respect to .

08

(1) State formula for expectation given .

---

(2) Note that is fixed inside the conditional expectation.

• Treat as inside integral.

---

(3) Prove the second formula.

---

(4) State final answer.

09

Let and .

10

(1) Find .

Note that this follows a binomial distribution with parameters .

Thus,

---

(2) Find using iterated expectation.

---

(3) Find

---

(4) Find covariance

---

(5) State final conclusions. Since the covariance is positive, and are positively correlated.