W02 Regular

Due date: Sunday 1/25, 11:59pm

Trig power products

01

04

All odd power product

Compute the integral:

Link to original

Solution

Solutions - 0040-04

(1) Notice odd power on . Swap the even bunch:

---

(2) Perform -sub setting and thus :

---

(3) Convert back to :

Link to original

02

05

Tangent and secant mixed parity

Compute the integral:

(a) Using .

(b) Using .

Link to original

Solution

Solutions - 0040-05

(a) Select and thus :

---

(b)

(1) Select and thus :

---

(3) Swap even bunch using :

---

(4) Perform -sub with and integrate:

Link to original

03

06

Power product with negative power

Compute the integral:

Link to original

Solution

Solutions - 0040-06

(1) Change variable by substituting and :

---

(2) Identify :

---

(3) Perform -sub with and thus :

Link to original

Trig substitution

04

03

Trig sub

Compute the integral:

Link to original

Solution

Solutions - 0050-03

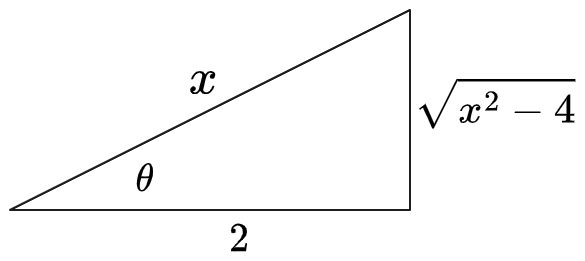
(1) Notice pattern, so we should make use of the identity .

Select and thus . Then:

Plug in and simplify:

(We must assume that for the relevant values of here.)

---

(2) Use power-to-frequency conversion:

---

(3) Convert back to terms of :

First draw a triangle expressing :

Therefore:

For , use the double-angle identity:

Therefore:

Link to original

05

04

Trig sub

Compute the integral:

Hint: complete the square and then substitute.

Link to original

Solution

Solutions - 0050-04

(1) Complete the square:

---

(2) Substitute and thus :

---

(3) Convert back to terms of :

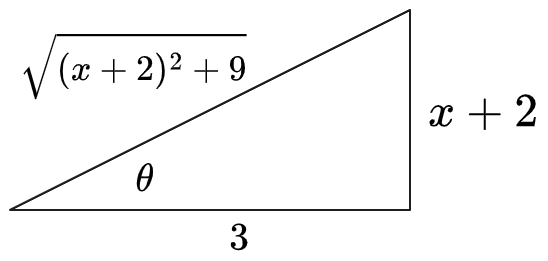
First draw a triangle expressing :

It follows that . Then:

---

Note A: Using log rules, the denominator can be brought out as which can be “absorbed” into the constant .

Link to original

06

05

Trig sub

Compute the integral:

Link to original

Solution

Solutions - 0050-05

(1) Notice pattern, so we should make use of the identity .

Select and thus . Then:

---

(2) Convert to and integrate:

---

(3) Convert back to terms of :

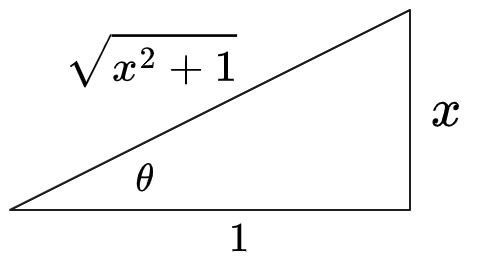
Draw a triangle expressing :

Therefore and . Then:

Link to original

07

06

Double sub: -sub then trig sub

Compute the definite integral:

Link to original

Solution

Solutions - 0050-06

(1) Perform -sub setting and thus . Adjust the bounds as follows:

Therefore:

---

(2) Notice pattern, so we should make use of the identity .

Select and thus . Adjust bounds:

Therefore:

---

(3) Integrate from memory or multiplying above and below by :

Link to original

08

07

Trig sub for electric charge

A charged wire lies on the -axis running from to . The electric field at the point is given by:

Find the numerical value of assuming and and and .

Link to original

Solution

Solutions - 0050-07

(1) Take out constants and insert given values:

---

(2) Notice pattern, so we should make use of the identity .

Select and thus . Then:

Adjust bounds:

Then:

---

(3) Integrate:

---

(4) Compute :

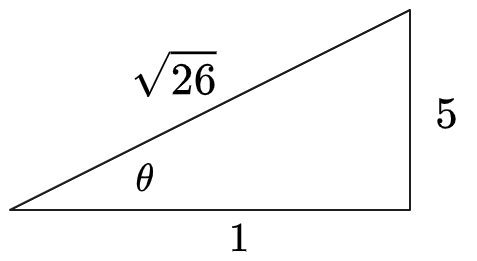
Draw a triangle expressing :

Therefore . Then:

Link to original