Stepwise problems - Thu. 11:59pm
Positive series
01
01
Link to originalIntegral Test (IT)
Use the Integral Test to determine whether the series converges:
Show your work. You must check that the test is applicable.
Solution
Series
02
03
Link to originalGeometric series
Compute the following summation values using the sum formula for geometric series.
(a)
(b)
Solution
Regular problems - Sun. 11:59pm
Sequences
03
06
Link to originalLimits and convergence
For each sequence, either write the limit value (if it converges), or write ‘diverges’.
(a)
(b) (c) (d) (e)
(f) (g) (h)
Solution
04
07
Link to originalLimits and convergence
For each sequence, either write the limit value (if it converges), or write ‘diverges’.
(a)
(b) (c) (d) (e)
(f) (g)
Solution
Series
05
04
Link to originalRepeating digits
Using the geometric series formula, find the fractional forms of these decimal numbers:
(a)
(b)
Solution
06
07
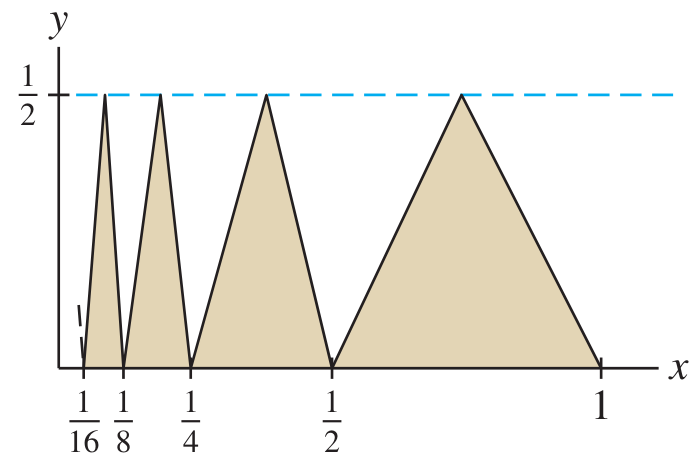
Link to originalTotal area of infinitely many triangles
Find the area of all the triangles as in the figure:
(The first triangle from the right starts at
, and going left they never end.)
Solution
07
02
Link to originalGeometric series
Compute the following summation values using the sum formula for geometric series.
(a)
(b)
Solution
Positive series
08
04
Link to originalIntegral Test (IT)
Determine whether the series is convergent by using the Integral Test.
Show your work. You must check that the test is applicable.
(a)
(b) (c)
Solution