Stepwise problems - Mon. Dec 1, 11:59pm
Complex algebra
01
01
Complex arithmetic
Write each of these expressions in the form
. (a)
(b) Link to originalSolution
01
(a)
(b)
Link to original
02
02
Complex solutions of quadratic equations
Find all solutions and write them in the form
. Solution
02
The quadratic formula provides all complex roots, using that
: Link to original
Regular problems - Thu. Dec 4, 11:59pm
Calculus with polar curves
03
03
Polar curve - Slope of tangent line
Find the slope of the tangent line to the given polar curve:
Hint: First determine parametric Cartesian coordinate functions using
as the parameter. Link to originalSolution
03
First convert this polar curve to a parametric curve using
and : Then use
. Differentiate: Therefore:
Link to original
04
04
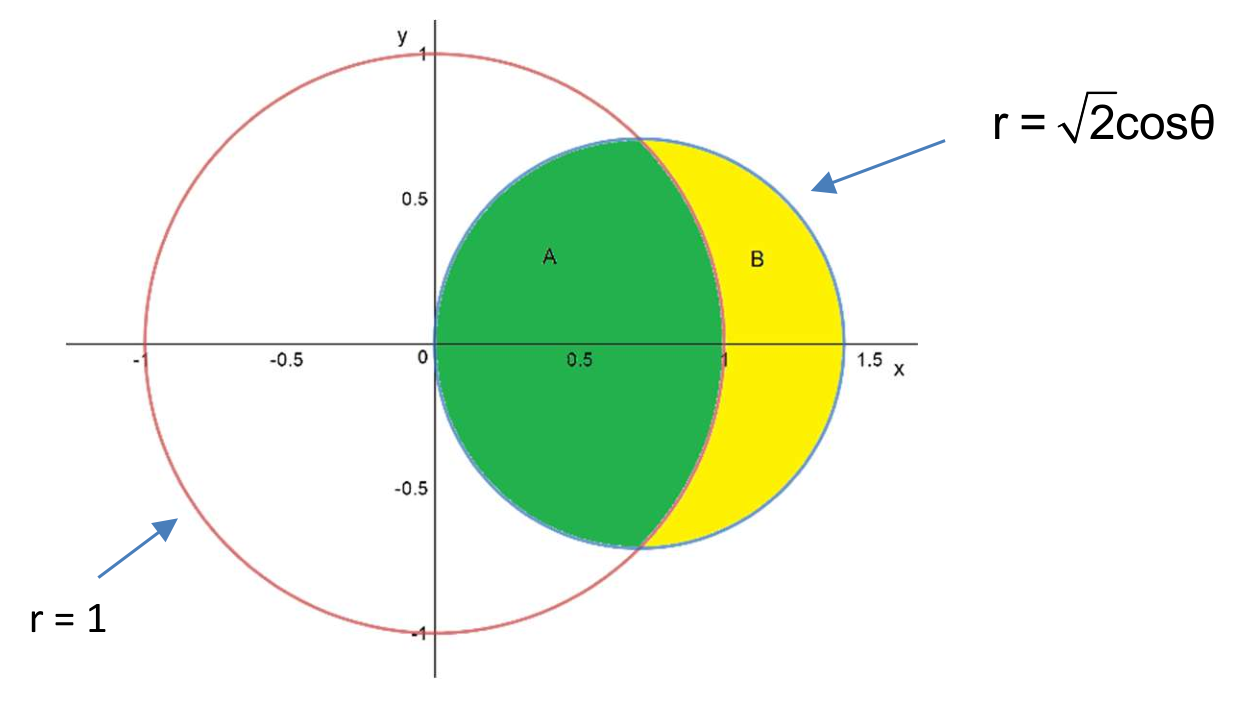
Polar coordinates - lunar areas
(a) Find the area of the green region.
(b) Find the area of the yellow region.
(You can find these in either order.)
Link to originalSolution
04
(a) Find the angle of the line from the origin to the point of intersection of the two curves (in Quadrant I):
Compute the area below this line, inside the larger circle, and above the
-axis: (This circular sector is also just
of the whole disk area, which is .) Compute the area above the line and inside the smaller circle:
Combined area in green above the
-axis is . Double this for the total green area:
(b) Notice that green and yellow combine to give the area of the smaller circle. The area of the smaller circle is
. Therefore, the yellow region has area:
Note: It is also reasonable to find the yellow region first, using this formula:
Link to original
05
05
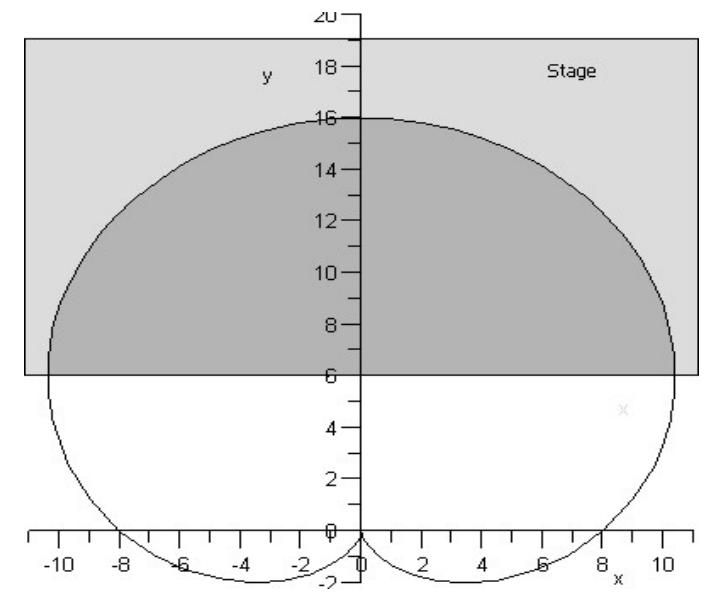
Pickup region of a microphone - limaçon area
The pickup region of a microphone is described by a limaçon with equation
, and part of the region is on a stage. Find the area of the part of the region on the stage.
Link to originalSolution
05
Find the intersection between the line
and the curve, in Quadrant I: Of course
, so we have and (in Quadrant I) therefore . To get the answer, we double the area from this angle up to the vertical : Link to original
06
02
Arclength of one loop of a rose
Consider the graph of the polar curve
. Set up an integral which computes the arclength of one loop of this curve.
Link to originalSolution
06
Solve for consecutive (in
) solutions to to get the starting and ending for a single loop: Integrate:
Link to original
07
06
Area of an inner loop
A limaçon is given as the graph of the polar curve
. Find the area of the inner loop of this limaçon.
Link to originalSolution
07
Solve for consecutive (in
) solutions to to get the starting and ending for a single loop: The interval
corresponds to the inner loop. To see this, draw a graph of the limaçon: Link to original
Complex algebra
08
03
Complex arithmetic
Write each of these expressions in the form
. (a)
(b) Solution
08
(a)
(b)
The correct interpretation is
and and therefore . It would not be correct to write
. Each instance of the symbol “
Link to original” involves making a choice of root. There are possible choices.
09
04
Complex solutions of quadratic equations
Find all solutions and write them in the form
. (a)
(b) Solution
09
(a)
(b)
Link to original