Unit 04 - Essential problems

Parametric curves

01

Convert parametric curve to function graph

Write the following curves as the graphs of a function . (Find for each case.)

(a) , and

(b) , and

Sketch each curve.

Link to original

03

Convert function graph to parametric curve

Find parametric curves whose images are the following graphs:

(a) and

(b) and

Link to original

03

Parametric concavity

Find the interval(s) of on which the parametric curve is concave up.

Link to original

06

Cycloid - Arclength and surface area of revolution

Consider the cycloid given parametrically by .

(a) Find the length of one arch of the cycloid.

(b) Suppose one arch of the cycloid is revolved around the -axis. Find the area of this surface of revolution.

Link to original

Polar curves

01

Convert points: Cartesian to Polar

Convert the Cartesian (rectangular) coordinates for these points into polar coordinates:

(a) (b) (c) (d)

Link to original

01

Polar curve - Vertical or horizontal tangent lines

Find all points on the given curve where the tangent line is horizontal or vertical.

Hint: First determine parametric Cartesian coordinate functions using as the parameter.

Link to original

04

Convert equations: Cartesian to Polar

Convert the Cartesian equation to a polar equation. Be sure to simplify.

(a) (b) (c)

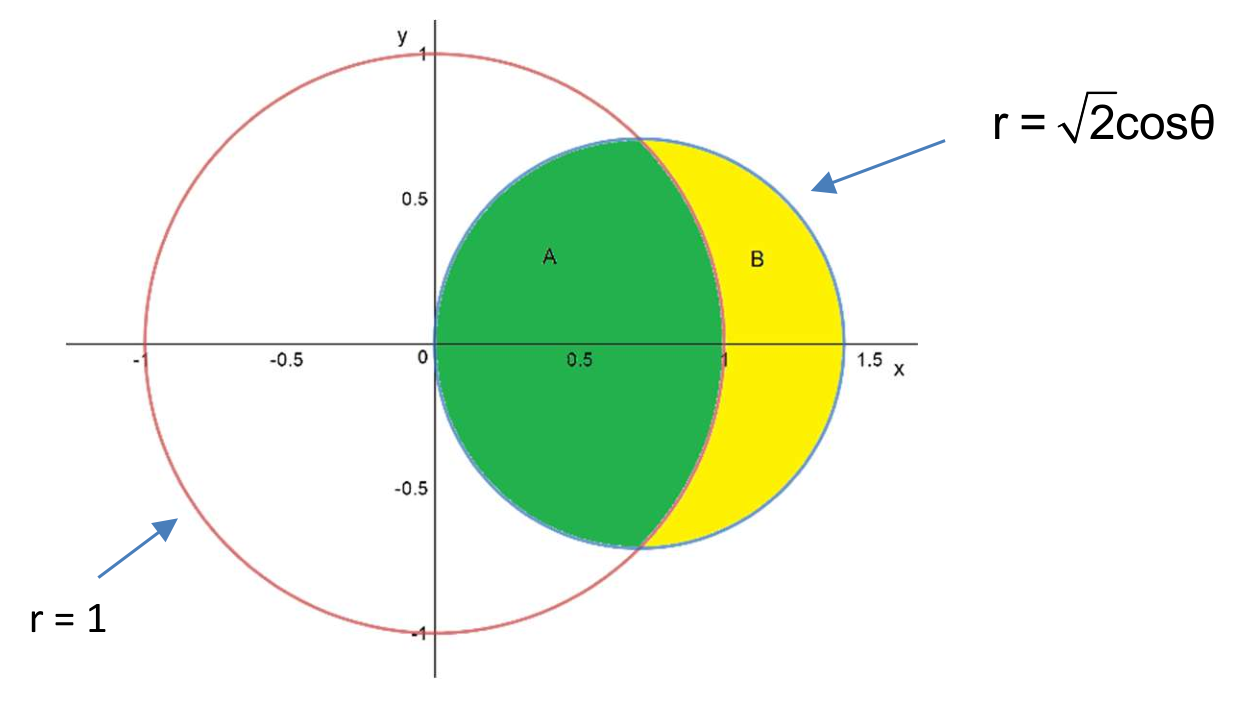
Link to original

04

Polar coordinates - lunar areas

(a) Find the area of the green region.

(b) Find the area of the yellow region.

(You can find these in either order.)

Link to original

06

Area of an inner loop

A limaçon is given as the graph of the polar curve .

Find the area of the inner loop of this limaçon.

Link to original

Complex numbers

01

Complex forms - exponential to Cartesian

Write each number in the form .

(a) (b)

Link to original

04

Complex products and quotients using polar

For each pair of complex numbers and , compute:

(a)

(b)

(Use polar forms with .)

Link to original

05

Complex powers using polar

Using De Moivre’s Theorem, write each number in the form .

(a) (b)

(First convert to polar/exponential, then compute the power, then convert back.)

Link to original

02

Complex roots using polar

Find each of the indicated roots.

(a) The four roots of .

(b) The three cube () roots of .

Try to write your answer in form if that is not hard, otherwise leave it in polar form.

Link to original