More calculus with parametric curves
01 Theory - Arclength
Theory 2
Arclength formula
The arclength of a parametric curve with coordinate functions
and is: This formula assumes the curve is traversed one time as
increases from to . Counts total traversal
This formula applies when the curve image is traversed one time by the moving point.
Sometimes a parametric curve traverses its image with repetitions. The arclength formula would add length from each repetition!
Link to originalExtra - Derivation of arclength formula
The arclength of a parametric curve is calculated by integrating the infinitesimal arc element:
In order to integrate
in the variable, as we must for parametric curves, we convert to a function of : So we obtain
and the arclength formula follows from this:
02 Illustration
Example - Perimeter of a circles
Perimeter of a circle
(1) The perimeter of the circle
is easily found. We have , and therefore:
(2) Integrate around the circle:
Link to original
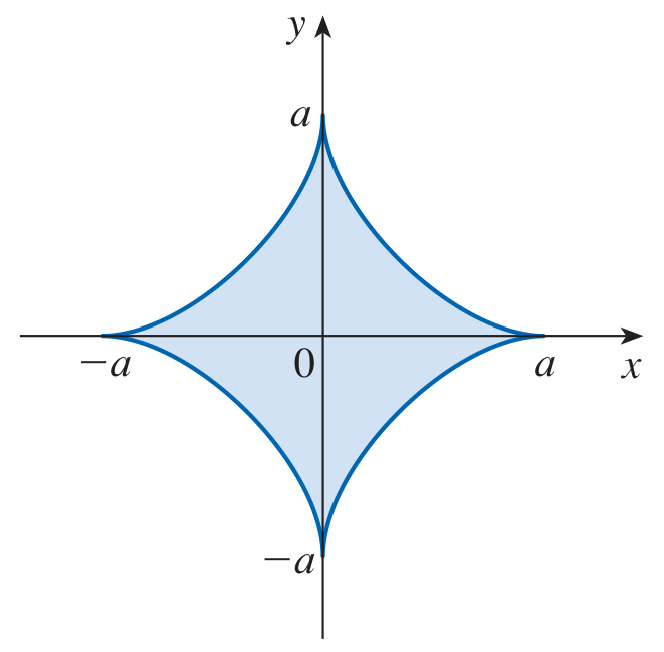
Example - Perimeter of an asteroid
Perimeter of an asteroid
Find the perimeter length of the ‘asteroid’ given parametrically by
for .
Solution
(1) Notice: Throughout this problem we use the parameter
instead of . This does not mean we are using polar coordinates! Compute the derivatives in
:
(2) Compute the infinitesimal arc element.
Plug into the arc element, simplify:
(3) Bounds of integration?
Easiest to use
. This covers one edge of the asteroid. Then multiply by 4 for the final answer. On the interval
, the factor is positive. So we can drop the absolute value and integrate directly. Absolute values matter!
If we tried to integrate on the whole range
, then really does change sign. To perform integration properly with these absolute values, we’d need to convert to a piecewise function by adding appropriate minus signs.
(4) Integrate the arc element:
Finally, multiply by 4 to get the total perimeter:
Link to original
03 Theory - Distance, speed
Theory 3
Distance function
The distance function
returns the total distance traveled by the particle from a chosen starting time up to the (input) time : We need the dummy variable
so that the integration process does not conflict with in the upper bound.
Speed function
The speed of a moving particle is the rate of change of distance:
This formula can be explained in either of two ways:
Link to original
- Apply the Fundamental Theorem of Calculus to the integral formula for
. - Consider
for a small change : so the rate of change of arclength is , in other words .
04 Illustration
Example - Speed, distance, displacement
Speed, distance, displacement
The parametric curve
describes the position of a moving particle ( measuring seconds). (a) What is the speed function? Suppose the particle travels for
seconds starting at . (b) What is the total distance traveled? (c) What is the total displacement? Solution
(a)
Compute derivatives:
Now compute the speed:
(b)
Distance traveled by using speed.
Compute total distance traveled function:
Substitute
and . New bounds are and . Calculate: The distance traveled up to
is:
(c)
Displacement formula:
Now compute starting and ending points.
For starting point, insert
: For ending point, insert
: Insert
and : Link to original
05 Theory - Surface area of revolutions
Theory 4
Surface area of a surface of revolution: thin bands
Suppose a parametric curve
is revolved around the -axis or the -axis. The surface area is:
The radius
should be the distance to the axis: This formulas adds the areas of thin bands, but the bands are demarcated using parametric functions instead of input values of a graphed function.
The formula assumes that the curve is traversed one time as
Link to originalincreases from to .
06 Illustration
Example - Surface of revolution - parametric circle
Surface of revolution - parametric circle
By revolving the unit upper semicircle about the
-axis, we can compute the surface area of the unit sphere. Parametrization of the unit upper semicircle:
Therefore, the arc element:
Now for
we choose because we are revolving about the -axis.
Plugging all this into the integral formula and evaluating gives:
Notice: This method is a little easier than the method using the graph
Link to original.
Example - Surface of revolution - parametric curve
Surface of revolution - parametric curve
Set up the integral which computes the surface area of the surface generated by revolving about the
-axis the curve for . Solution
For revolution about the
-axis, we set . Then compute
: Therefore the desired integral is:
Link to original
Polar curves
Videos
Review Videos
Videos, Organic Chemistry Tutor
Link to original
07 Theory - Polar points, polar curves
Theory 1
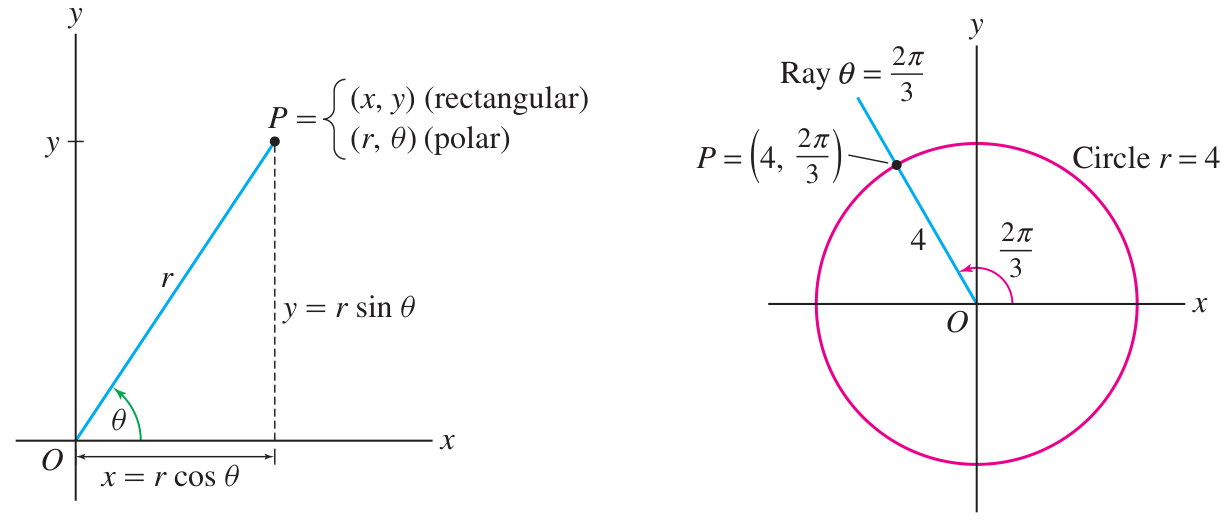
Polar coordinates are pairs of numbers
which identify points in the plane in terms of distance to origin and angle from -axis:
Converting
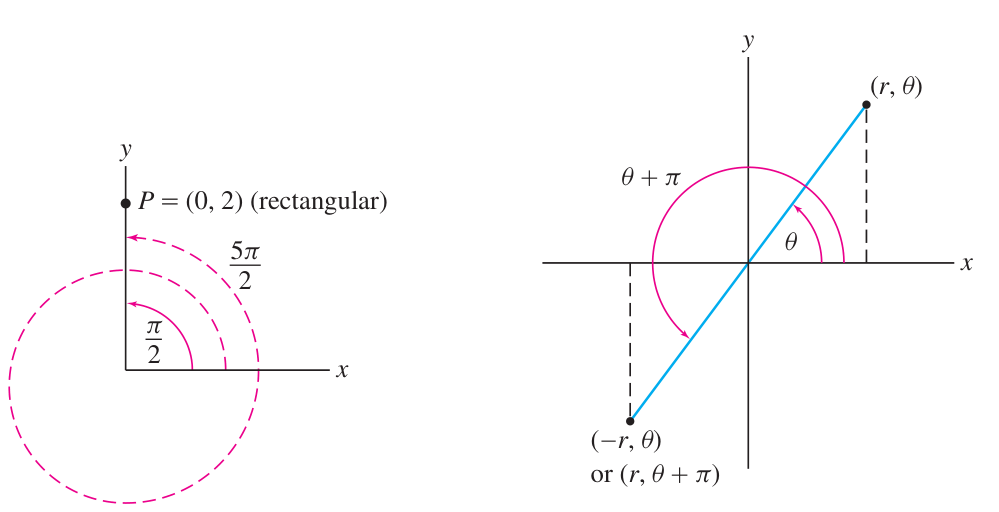
Polar coordinates have many redundancies: unlike Cartesian which are unique!
- For example:
- And therefore also
(negative can happen) - For example:
for every - For example:
for any Polar coordinates cannot be added: they are not vector components!
- For example
- Whereas Cartesian coordinates can be added:
The transition formulas
require careful choice of .
- The standard definition of
sometimes gives wrong
- This is because it uses the restricted domain
; the polar interpretation is: only points in Quadrant I and Quadrant IV (SAFE QUADRANTS) - Therefore: check signs of
and to see which quadrant, maybe need -correction!
- Quadrant I or IV: polar angle is
polar angle is
Equations (as well as points) can also be converted to polar.
For
, look for cancellation from . For
, try to keep inside of trig functions.
- For example:
Link to original
08 Illustration
Example - Converting to polar:
-correction Converting to polar: pi-correction
Compute the polar coordinates of
and of . Solution
For
we observe first that it lies in Quadrant II. Next compute:
This angle is in Quadrant IV. We add
to get the polar angle in Quadrant II: The radius is of course
since this point lies on the unit circle. Therefore polar coordinates are . For
we observe first that it lies in Quadrant IV. (No extra needed.) Next compute:
So the point in polar is
Link to original.
Example - Shifted circle in polar
Shifted circle in polar
For example, let’s convert a shifted circle to polar. Say we have the Cartesian equation:
Then to find the polar we substitute
and and simplify: So this shifted circle is the polar graph of the polar function
Link to original.