Arc length
01
Link to originalArc length - reversed
and roles Find the arc length of the curve that satisfies the equation
over .
Surface areas of revolutions - thin bands
02
Link to originalSurface area: revolved cubic
The curve
over is revolved around the -axis. Find the area of the resulting surface.
06
Link to originalSurface area: parabolic reflector
A parabolic reflector is given by rotating the curve
around the -axis for . What is the surface area of this reflector?
Hydrostatic pressure
05
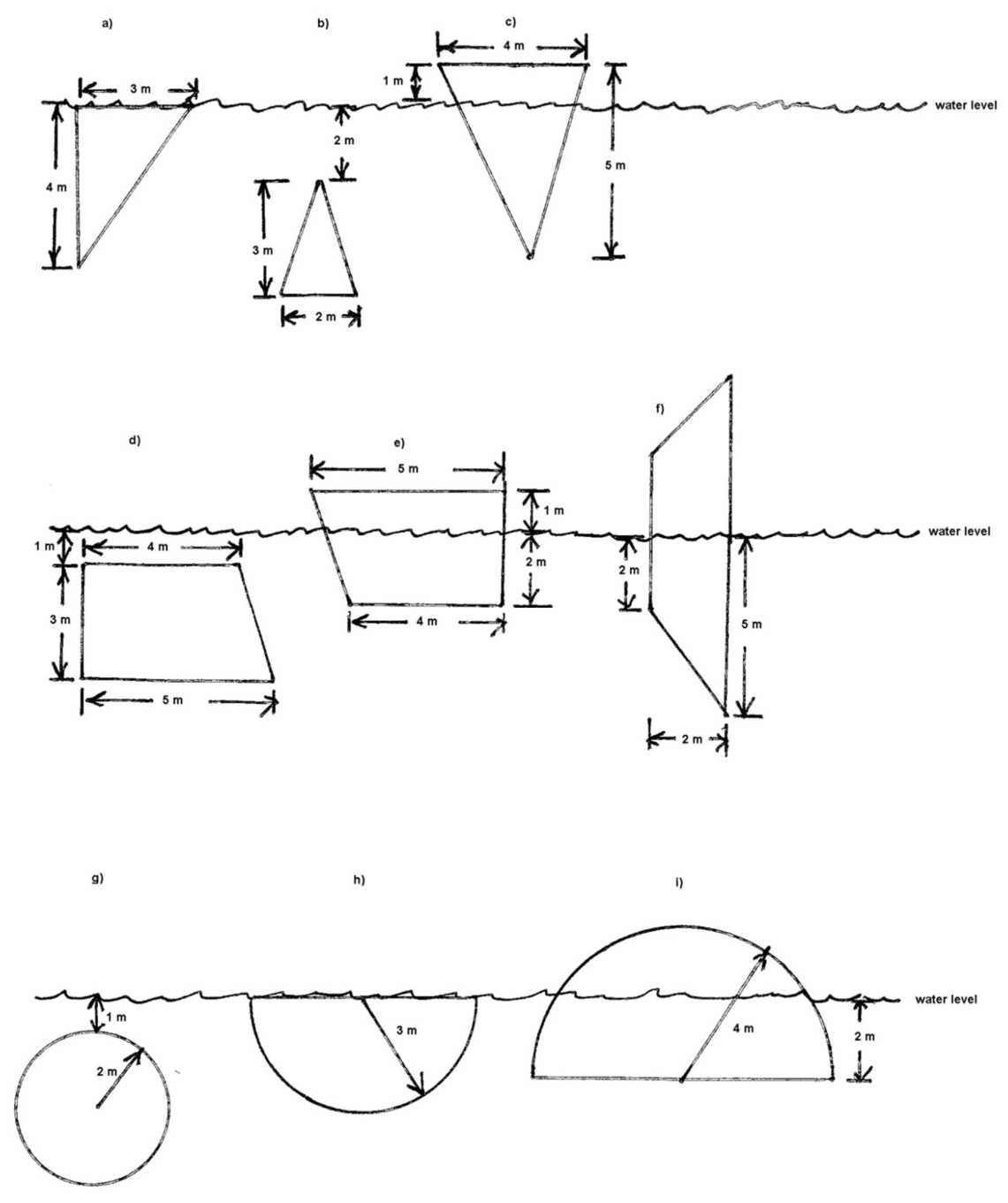
Link to originalFluid force on various plates
For diagrams (a)-(i) below, set up an integral to compute the hydrostatic force on the plate.
Moments and CoM
02
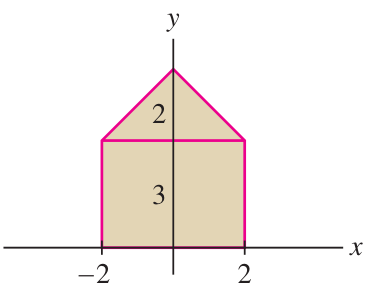
Link to originalCenter of mass of a house
A “house” is the region bounded by the (non-regular) pentagon with vertex points at
, , , , . Find the CoM of the house using additivity of moments.
03
Link to originalCoM of region between curves
Find the CoM of the region between the graph of
and the graph of over .
Work performed
01
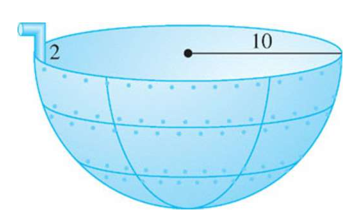
Link to originalPumping water from hemispherical tank
A hemispherical tank (radius
) is full of water. A pipe allows water to be pumped out, but requires pumping up above the top of the tank.
- (a) Set up an integral that computes the total work required to pump all the water out of the tank, assuming it is completely full.
- (b) Now assume the tank start out full just to
. What does the integral become?
02
Link to originalBuilding a conical tower
Set up an integral that computes the work done (against gravity) to build a circular cone-shaped tower of height
and base radius out of a material with mass density .
04
Link to originalWork to raise a leaky bucket
A bucket of water is raised by a chain to the top of a
-foot building. The water is leaking out, and the chain is getting lighter. The bucket weighs
, the initial water weighs , and the chain weighs , and the water is leaking at a rate of as the bucket is lifted at a rate of . What is the total work required to raise the bucket of water?
Improper integrals
03
Link to originalComparison test
Use the comparison test to determine whether the integral converges:
10
Link to originalComputing improper integrals, Part II
For each integral below, give the limit interpretation of improper integral and then compute the limit. Based on that result, state whether the integral converges. If it converges, what is its value?
- (a)
- (b)
- (c)