W02 Stepwise

Due date: Thursday 1/22, 11:59pm

Trig power products

01

01

Somewhat odd power product

Compute the integral:

Link to original

Solution

Solutions - 0040-01

(1) Notice odd power on . Swap the even bunch:

---

(2) Integrate with -sub setting and thus :

Link to original

02

02

Tangent and secant both even

Compute the integral:

Link to original

Solution

Solutions - 0040-02

Notice . Therefore integrate with -sub setting and :

Link to original

03

03

All even power product

Compute the integral:

Link to original

Solution

Solutions - 0040-03

(1) Notice all even powers. Use power-to-frequency conversion:

Plug in:

Simplify:

---

(2) Reduce power again for :

(This is derived from the power-to-frequency formula by changing ‘’ to ‘’ in that formula.)

---

(3) On the last term, swap even bunch:

Plug all in and obtain:

---

(4) Integrate the first three terms:

---

(5) Integrate the last term with -sub, setting and :

---

(6) Combine in final result:

Note: It is also possible to rewrite using trig identities. So, equally valid answers may look different than this.

Link to original

Trig substitution

04

01

Trig sub

Compute the definite integral:

Link to original

Solution

Solutions - 0050-01

(1) Substitute and thus . Adjust the bounds as follows:

Rewrite the integral:

---

(2) Use power-to-frequency conversion:

---

Note A: Use , then and this equals for .

Link to original

05

02

Trig sub

Compute the integral:

Link to original

Solution

Solutions - 0050-02

(1) Trig substitution. Notice , so we should make use of the identity .

Pick and thus .

Then:

Plug in:

(We assume that for the relevant values of .)

---

(2) Perform integration.

Either recall from memory, or multiply above and below by , and obtain:

---

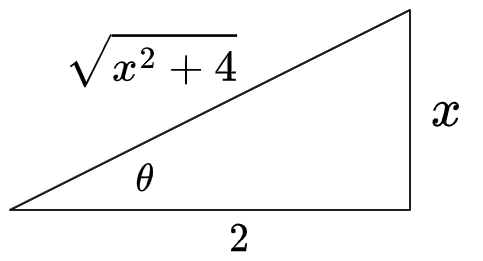
(3) To convert to we need given that .

Draw triangle expressing :

Therefore . We already know . Thus:

---

(4) Simplify with log rules:

Link to original