Stepwise problems - Thu. 11:59pm
Hydrostatic pressure
01
01
Link to originalFluid force on a triangular plate
Find the total force on the submerged vertical plate that is an isosceles triangle with (bottom) base
and height , and assume it is submerged with the upper vertex below the surface. Liquid is oil with density .
Solution
02
04
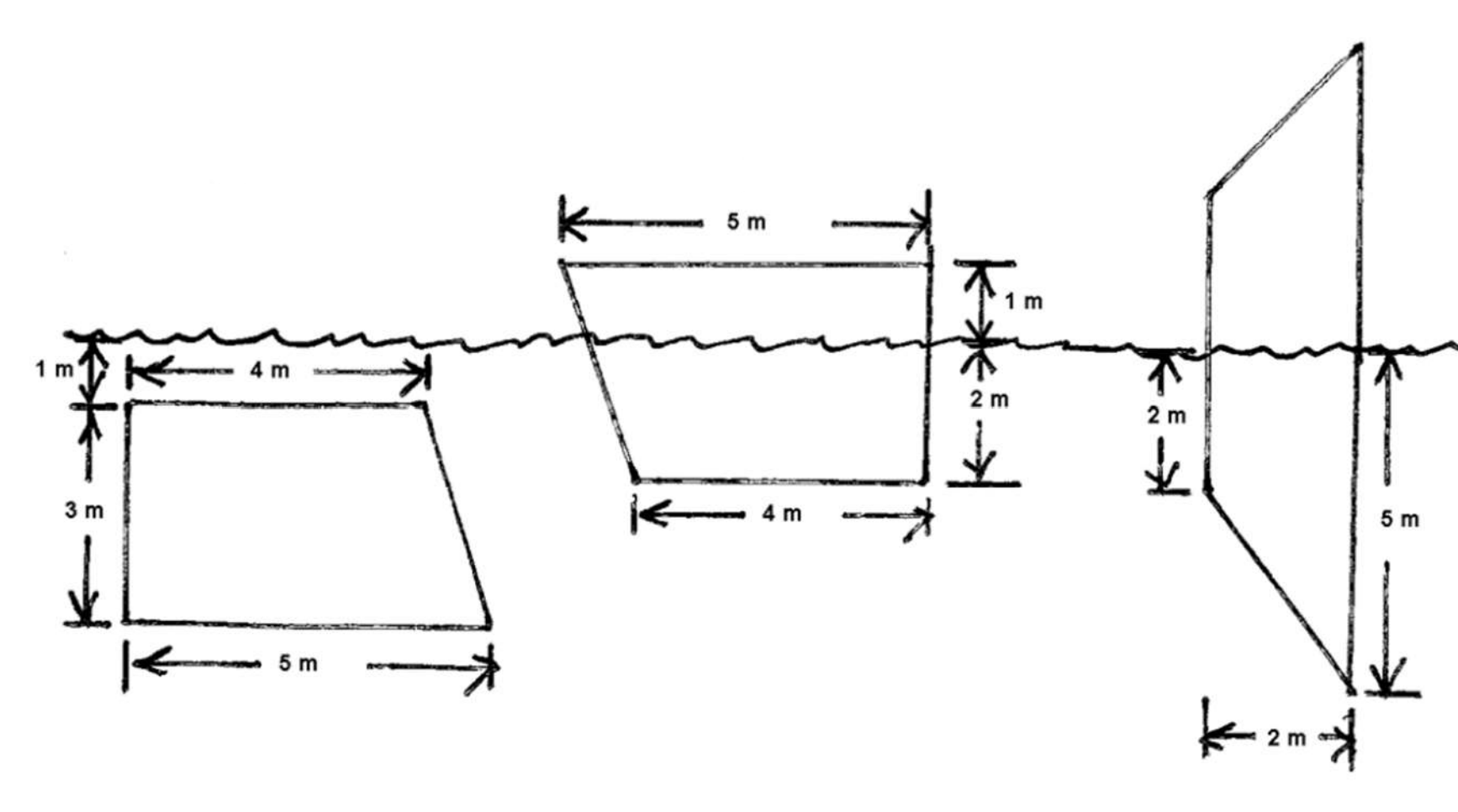
Link to originalFluid force on trapezoidal plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Solution
Work performed
03
01
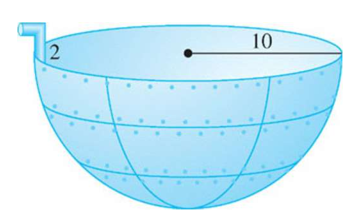
Link to originalPumping water from hemispherical tank
A hemispherical tank (radius
) is full of water. A pipe allows water to be pumped out, but requires pumping up above the top of the tank.
(a) Set up an integral that expresses the total work required to pump all the water out of the tank, assuming it is completely full.
(b) Now assume the tank start out full just to
. What does the integral become?
Solution
04
02
Link to originalBuilding a conical tower
Set up an integral that expresses the work done (against gravity) to build a circular cone-shaped tower of height
and base radius out of a material with mass density .
Solution
Regular problems - Sun. 11:59pm
Hydrostatic pressure
05
02
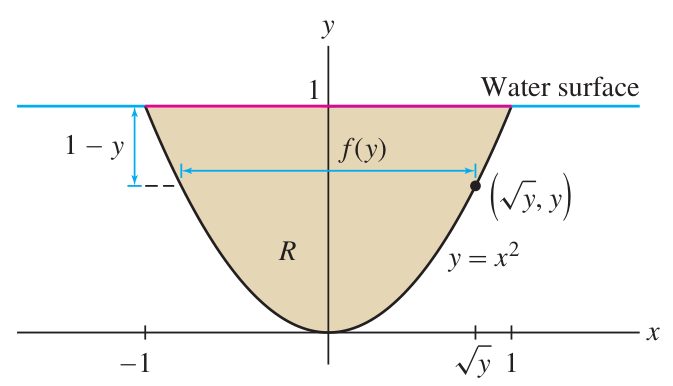
Link to originalFluid force on a parabolic plate
A parabolic plate is submerged vertically in water as in the figure:
The shape of the plate is bounded below by
and above by the line . (Note that increases going up in this coordinate system.) Compute the total fluid force on this plate.
(Hint: your integrand should contain
as a factor.)
Solution
06
03
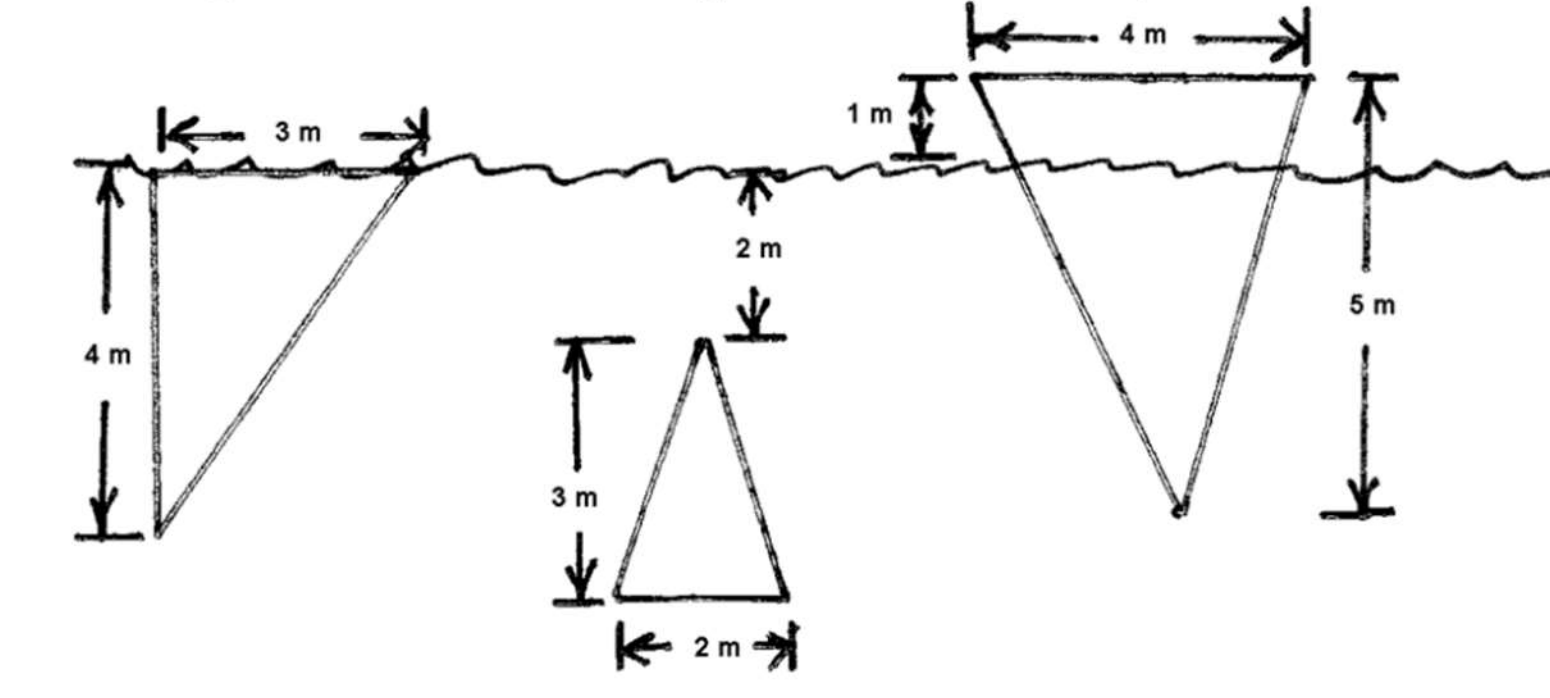
Link to originalFluid force on triangular plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Solution
07
05
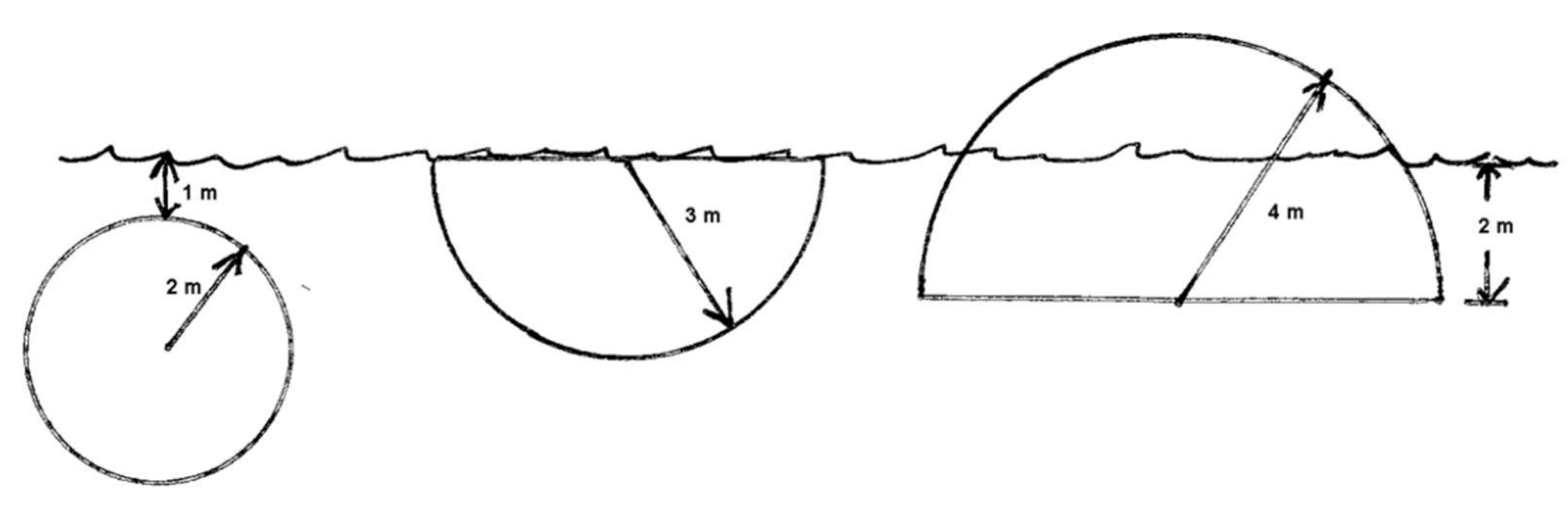
Link to originalFluid force on circular plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Solution
Work performed
08
03
Link to originalWork to raise a leaky bucket
A bucket of water is raised by a chain to the top of a
-foot building. The water is leaking out, and the chain is getting lighter. The bucket weighs
, the initial water weighs , and the chain weighs , and the water is leaking at a rate of as the bucket is lifted at a constant rate of . What is the total work required to raise the bucket of water?
Solution
09
04
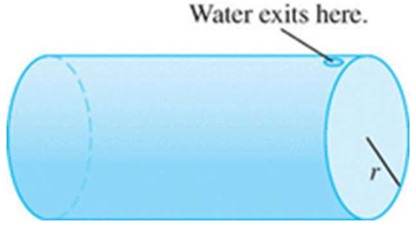
Link to originalWork to pump water from cylindrical tank
A cylindrical tank is full of water and the water is pumped out the top. (See figure.) The length of the tank is
and the radius is .
(a) Set up an integral for the total work performed assuming the tank is initially completely full.
(b) Set up an integral for the total work performed assuming the tank is initially full to
and the water is pumped out of a spigot extending above the top of the tank.
Solution
10
05
Link to originalWork to build a pyramid
The Great Pyramid of Giza is
tall and has a square base with on each side. It is built of stone with mass density . Set up an integral that expresses the work (against gravity) required to build the pyramid.
Solution