W14 - Homework

means: “eligible for Friday Presentation”

Stepwise problems - Sun. Nov 23, 11:59pm

Polar curves

01

01

Convert points: Cartesian to Polar

Convert the Cartesian (rectangular) coordinates for these points into polar coordinates:

(a) (b) (c) (d)

Solution

01

(a)

Q1, SAFE, .

---

(b)

Q1, SAFE, .

---

(c)

Q2, UNSAFE, and we add to this angle.

---

(d)

Q2, UNSAFE, (use 30-60-90 triangle) and we add to this angle.

Link to original

Link to original

02

02

Convert equations: Polar to Cartesian

Convert the polar equation to a Cartesian equation. Be sure to simplify.

(a) (b) (c)

Solution

02

(a)

---

(b)

Use and therefore:

So:

This is a circle centered at with radius .

---

(c)

Using and :

Note: This assumes that .

Link to original

Link to original

Calculus with polar curves

03

01

Polar curve - Vertical or horizontal tangent lines

Find all points on the given curve where the tangent line is horizontal or vertical.

Hint: First determine parametric Cartesian coordinate functions using as the parameter.

Solution

03

Observe that this parametric curve is a circle centered at with radius . So we expect vertical tangents at and horizontal tangents at .

Treat as the parameter. We always have . This equals here because . Since we can further simplify to .

Then .

Also .

---

To find vertical tangents, solve for :

Check that is not also zero at these points, else they would be stationary points:

Now find the Cartesian coordinates for these points:

---

To find the horizontal tangents, solve for :

Check that is not also zero at these points, else they would be stationary points:

Now find the Cartesian coordinates for these points:

Link to original

Link to original

Regular problems - Sun. Nov 30, 11:59pm

Polar curves

05

03

Convert points: Polar to Cartesian

Convert the polar coordinates for these points into Cartesian (rectangular) coordinates:

(a) (b) (c) (d)

Solution

04

(a)

---

(b)

Method 1:

First compute and . Then and .

Method 2:

Observe . Then , and obtain the answer.

---

(c)

---

(d)

Link to original

Link to original

06

04

Convert equations: Cartesian to Polar

Convert the Cartesian equation to a polar equation. Be sure to simplify.

(a) (b) (c)

Solution

05

(a) (b) (c)

(a)

Insert and :

---

(b)

---

(c)

Link to original

Link to original

07

05

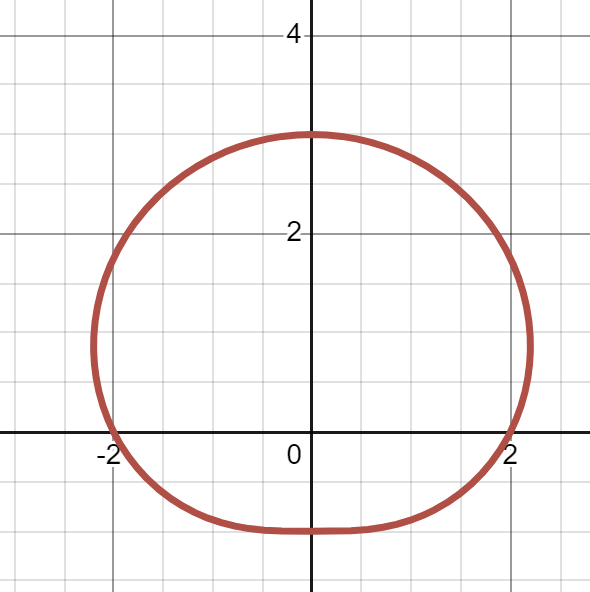
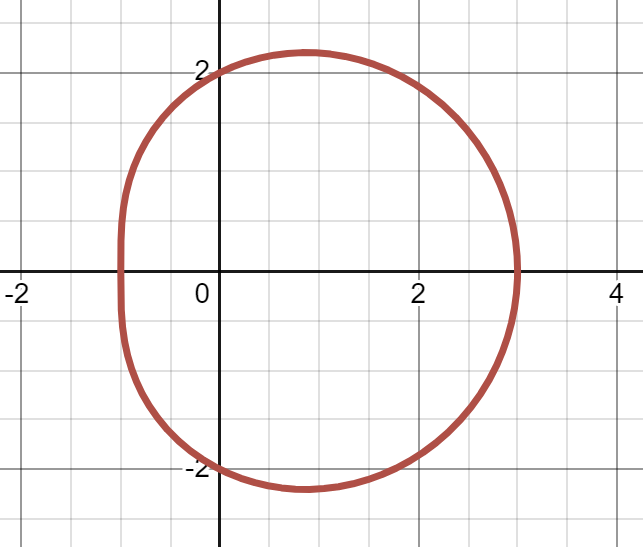
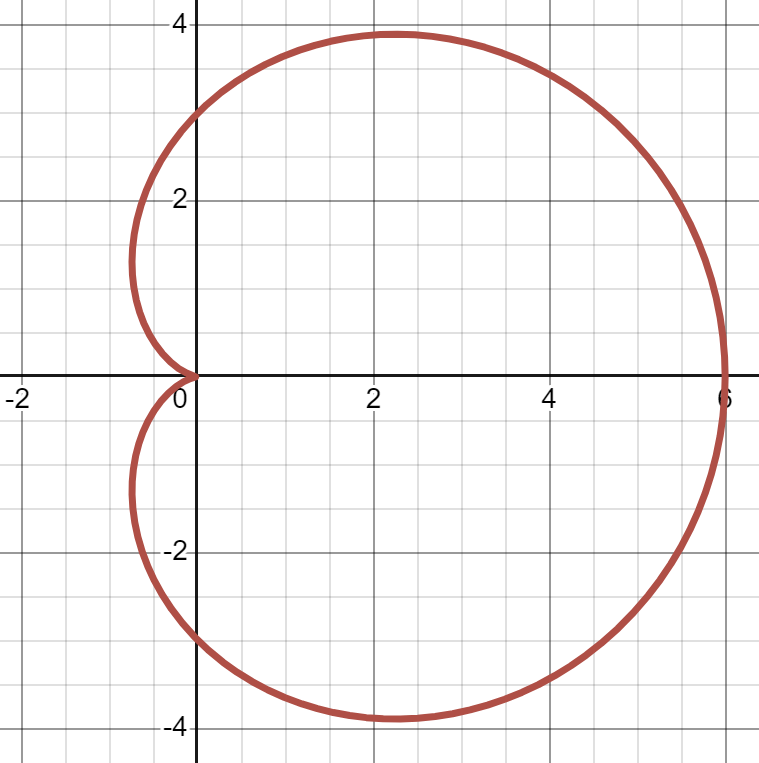
Sketching limaçons

Sketch the graphs of the following polar functions:

(a) (b)

(c) (d)

Solution

06

(a)

(b)

(c)

(d)

Link to original

Link to original

08

06

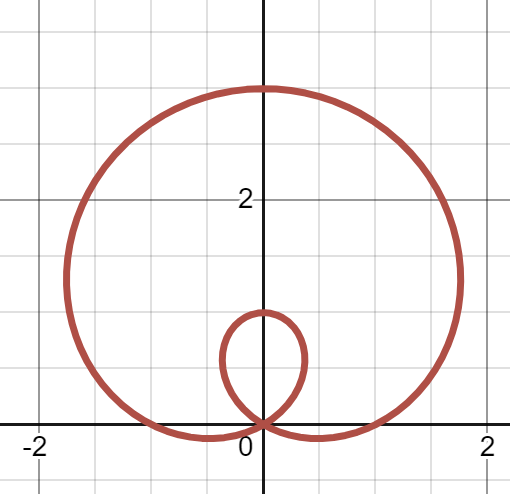
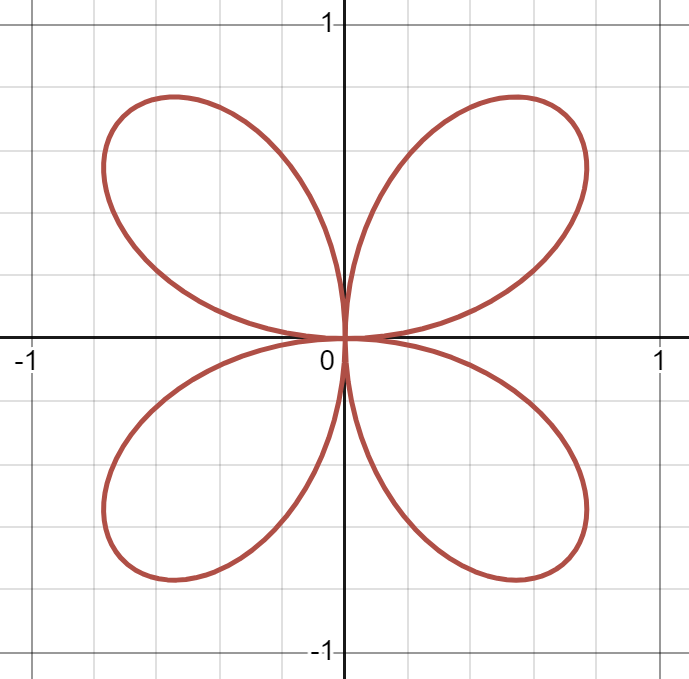
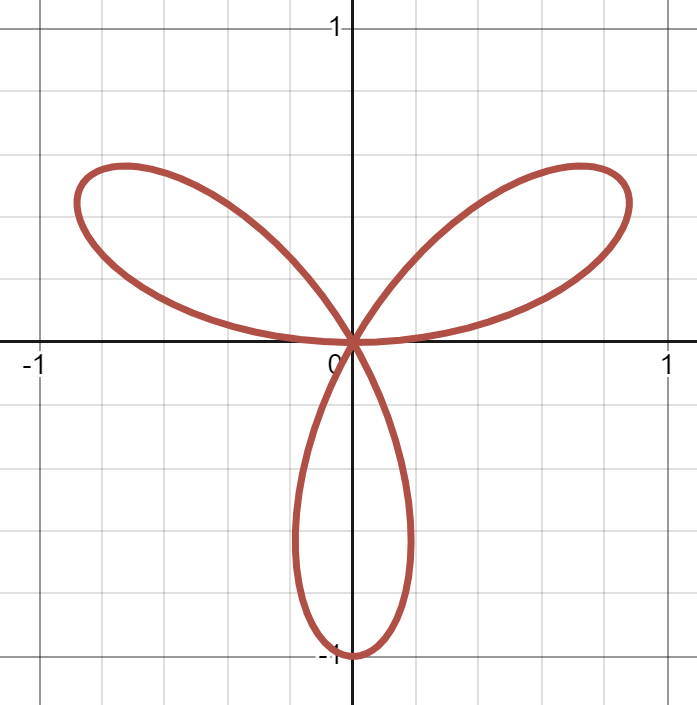
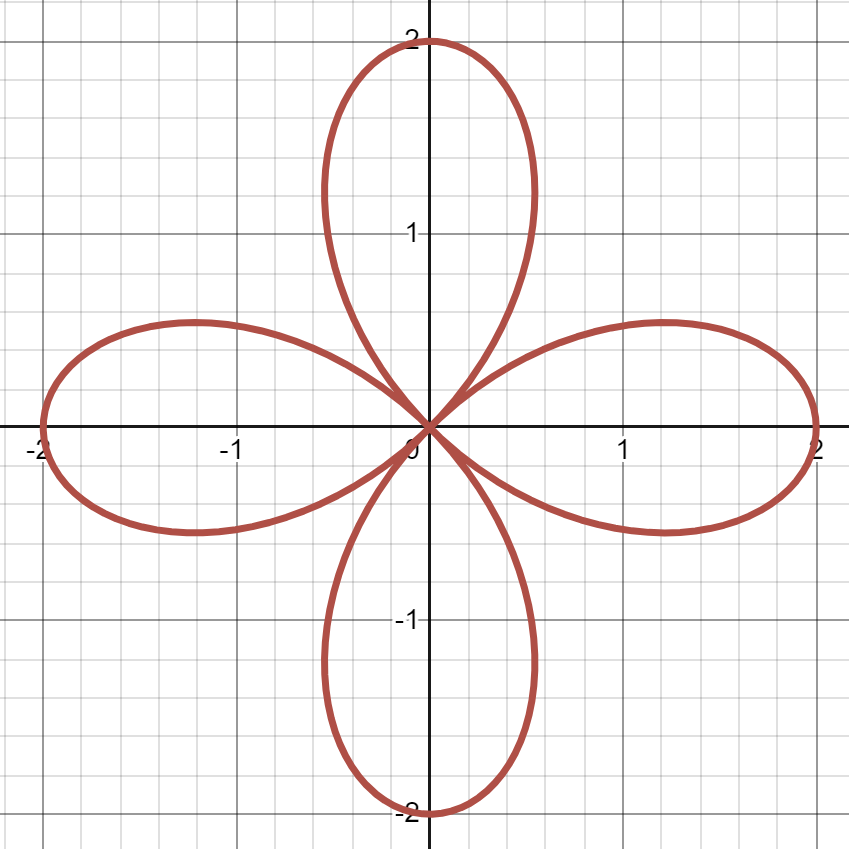
Sketching roses

Sketch the graphs of the following polar functions. Use numbers to label the order in which the leaves/loops are traversed.

(a) (b) (c)

Solution

07

(a)

Numbers should be placed on the loops, 1, 2, 3, 4, starting in Q1 and going clockwise.

(b)

Numbers should be placed on the loops, 1, 2, 3, starting in Q1 and going clockwise.

(c)

Numbers should be placed on the loops, 1, 2, 3, 4, starting on the -axis and going clockwise.

Link to original

Link to original

Calculus with parametric curves

09

05

Minimum speed of a particle

Suppose a travelling particle has position modelled by the parametric curve:

What is the slowest speed of the particle?

Solution

08

Derivatives:

Speed function:

Now we minimize this function as in Calc I.

Method 1:

Differentiate:

This equals zero if-and-only-if the numerator equals zero (assuming the denominator is not zero there):

Since is negative for and positive for , we may deduce that is the time of the minimal value of . So:

Method 2:

Instead of differentiating , we can look at its square , since the minimum of this will occur at the same time as the minimum of (because is a monotone increasing function). But becomes , and the rest of the solution proceeds as in Method 1.

Link to original

Link to original

10

06

Cycloid - Arclength and surface area of revolution

Consider the cycloid given parametrically by .

(a) Find the length of one arch of the cycloid.

(b) Suppose one arch of the cycloid is revolved around the -axis. Find the area of this surface of revolution.

Solution

09

(a)

One arch is formed from the range .

Compute :

Therefore .

Now recall a power-to-frequency formula, and use it in reverse:

Therefore:

---

(b)

Link to original

Link to original