Shells
01
Shells volume - offset graph,
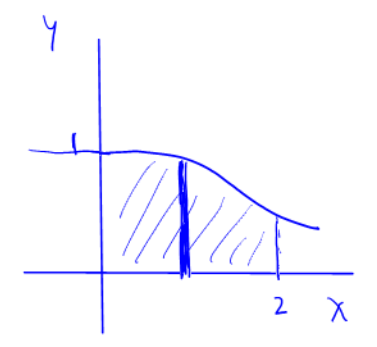
-axis Consider the region in the first quadrant bounded by the lines
, , , and the curve . Revolve this about the -axis. Find the volume of the resulting solid.
Link to originalSolution
01
(1) Set up integral.
(2) Perform
-substitution with and :
(3) Integrate with power rule:
Link to original
IBP
02
Integration by parts - A and T
Compute the integral:
Solution
03
(1) Select
and considering LIATE:
(2) Apply IBP formula
:
(3) Select another
and and do IBP again:
(4) Put all together in (A):
Note B: We can change notation
Link to originalto because the value of is arbitrary.
03
Integration by parts - A and L
Compute the integral:
Solution
06
(1) Select
and considering LIATE:
(2) Apply IBP formula
: Link to original
05
Integration by parts - A and I
Compute the integral:
Solution
08
(1) Select
and considering LIATE:
(2) Apply IBP formula
and compute integral:
(3) Perform
-sub with and :
(4) Insert result in Exp. (A):
Note B: We can change
Link to originalto because the inner expression is never negative.
Trig power products
01
Somewhat odd power product
Compute the integral:
Solution
01
(1) Notice odd power on
. Swap the even bunch:
(2) Integrate with
-sub setting and thus : Link to original
02
Tangent and secant both even
Compute the integral:
Solution
02
(1) Notice
. Therefore integrate with -sub setting and : Link to original
05
Tangent and secant mixed parity
Compute the integral:
- (a) Using
. - (b) Using
. Solution
07
(a) Select
and thus :
(b)
(1) Select
and thus :
(3) Swap even bunch using
:
(4) Perform
-sub with and integrate: Link to original
Trig subs
01
Trig sub
Compute the definite integral:
Solution
04
(1) Substitute
and thus . Adjust the bounds as follows: Rewrite the integral:
(2) Use power-to-frequency conversion:
Note A: Use
Link to original, then and this equals for .
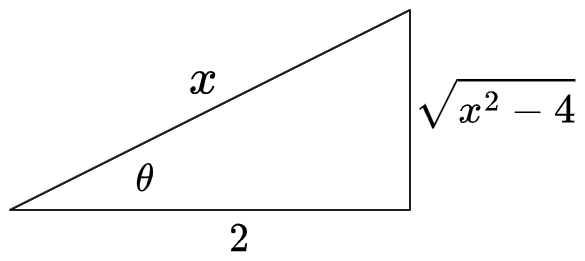
03
Trig sub
Compute the integral:
Solution
09
(1) Notice
pattern, so we should make use of the identity . Select
and thus . Then: Plug in and simplify:
(We must assume that
for the relevant values of here.)
(2) Use power-to-frequency conversion:
(3) Convert back to terms of
: First draw a triangle expressing
:
Therefore:
For
, use the double-angle identity: Therefore:
Link to original
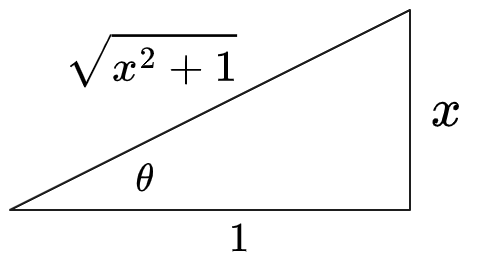
05
Trig sub
Compute the integral:
Solution
11
(1) Notice
pattern, so we should make use of the identity . Select
and thus . Then:
(2) Convert to
and integrate:
(3) Convert back to terms of
: Draw a triangle expressing
:
Therefore
and . Then: Link to original
Partial fractions
01
Distinct linear factors
Compute the integral:
Solution
01
(1) Write the partial fractions general form equation:
(2) Solve for constants.
Cross multiply:
Plug in
, obtain so . Plug in
, obtain so .
(3) Integrate each term:
Link to original
02
Long division first
Compute the integral:
Solution
02
(1) Numerator degree is not smaller! Long division first:
Now this already has the form of a partial fraction decomposition, so we proceed directly to integration.
(2) Integrate using power rule (with log):
Link to original
07
Partial fractions - linear and quadratic
Compute the integral:
Solution
08
(1) Denominator has degree 3, numerator has degree 2, therefore long division is not necessary.
(2) Write the partial fractions general form equation:
Notice that
is an irreducible quadratic (cannot be factored). So we have:
(3) Solve for constants:
Cross multiply:
Plug in
, obtain: Expand RHS:
Comparing
terms, obtain: and thus . Comparing constant terms,
.
(4) Integrate by terms:
Note A: For the last term, use the formula:
Link to original
08
Partial fractions - repeated factor
Compute the integral:
Solution
09
(1) Write the partial fractions general form equation:
Observe that
appears in degree 3 in the integrand, so we have one term for each power up to 3 in the partial fraction decomposition.
(2) Solve for constants:
Cross multiply:
Plug in
, obtain so . Plug in
, obtain . Plug in
, obtain: Plug in
, obtain:
(3) Integrate each term:
Optional simplification:
Link to original
Simpson’s Rule
02
Simpson’s Rule for volume by shells
Use Simpson’s Rule with
to compute the volume of the solid obtained by revolving the pictured region about the -axis. Can you do it without using a calculator?
Link to originalSolution
10
(1) Recall shells formula:
(2) Interpret:
Bounded above by
. Bounded below by -axis. Bounded left by
. Bounded right by . Obtain:
(3) Create table of values to apply Simpson’s Rule:
(4) Recall Simpson’s Rule formula:
Here
since in this formula represents the integrand values. Note that
. Plug in:
Therefore:
Therefore:
Link to original
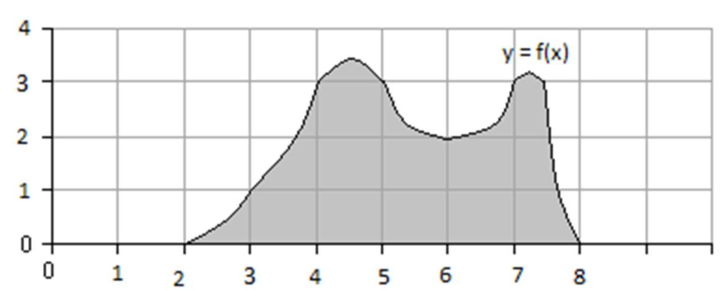
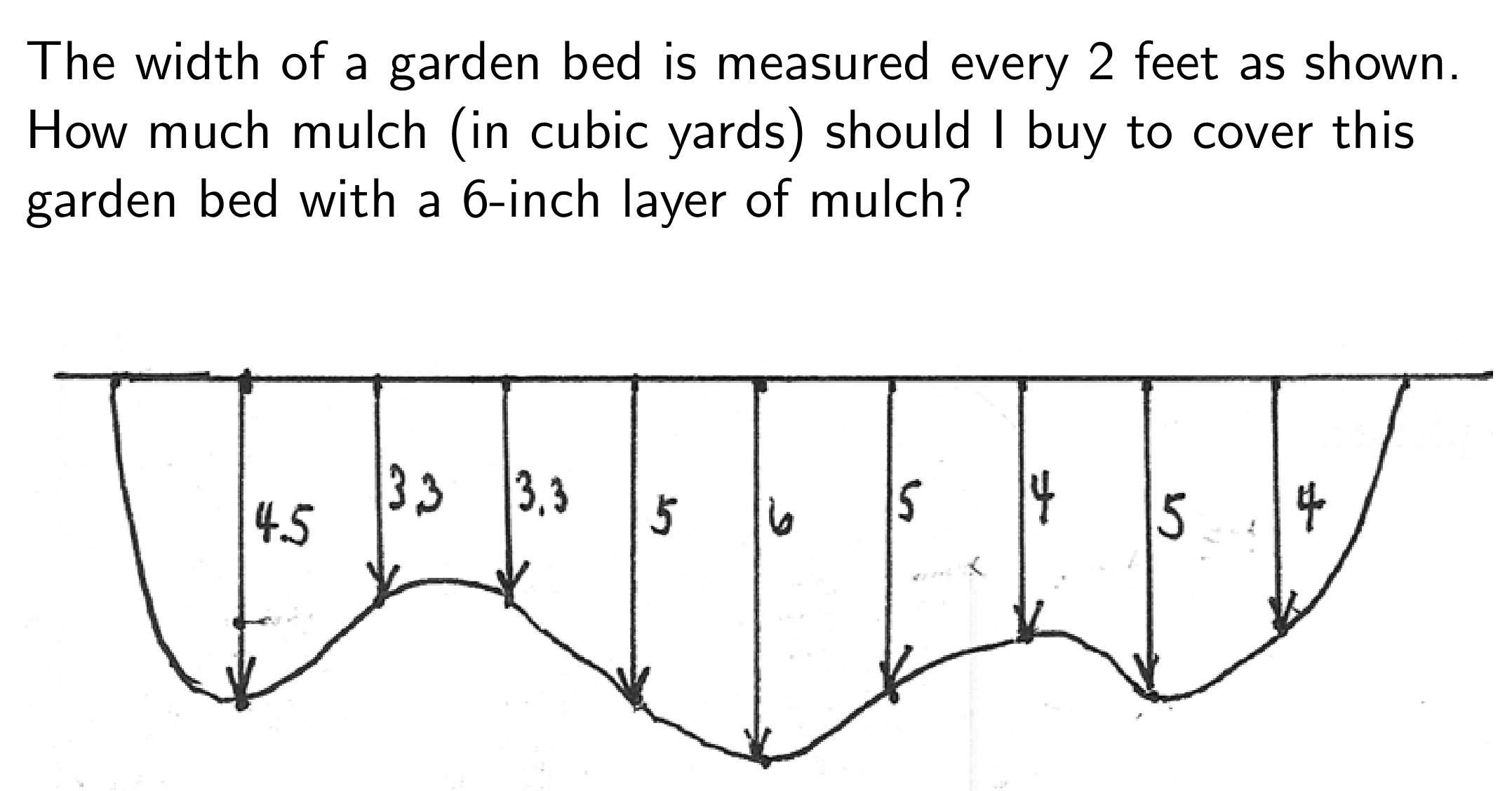
03
Area of a garden bed
Link to originalSolution
11
(1) Set up integration:
Set
at the left upper corner, with extending to the right, extending downwards. Then:
(2) Create table of values:
(3) Recall Simpson’s Rule formula:
Here
and . Thus:
(4) Compute cubic yards from known surface area:
Mulch is
deep, so the volume is: Link to original