Arc length
01
Arc length - reversed
and roles Find the arc length of the curve that satisfies the equation
over . Link to originalSolution
01
(1) Integral formula for arclength:
(2) Work out integrand:
(3) Integrate:
Link to original
Surface areas of revolutions - thin bands
01
Surface area: revolved cubic
The curve
over is revolved around the -axis. Find the area of the resulting surface.
Link to originalSolution
02
(1) Integral formula for surface area, revolution about
-axis:
(2) Work out integrand:
Then:
So:
(3) Perform
-sub with and so :
(4) Integrate:
Link to original
03
Surface area: parabolic reflector
A parabolic reflector is given by rotating the curve
around the -axis for . What is the surface area of this reflector?
Link to originalSolution
06
Method 1: integrate in
(1) Integral formula for surface area:
(2) Integrate: perform
-sub with and so :
Method 2: integrate in
(1) Integral formula for surface area using
:
(2) Integrate: perform
-sub with and so : Link to original
Hydrostatic pressure
03
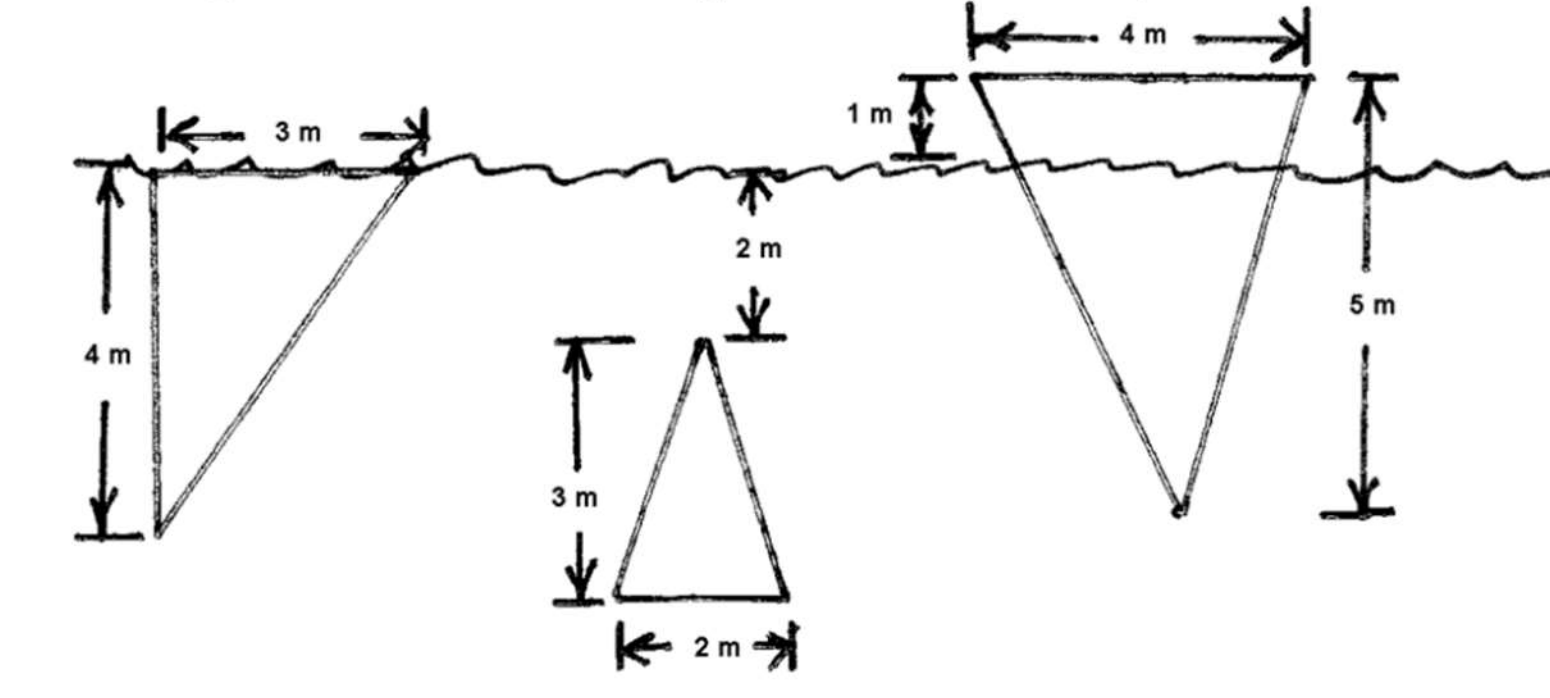
Fluid force on triangular plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Link to originalSolution
06
(1) Integral formula:
Option 1:
(2) Using
at water line, increasing downwards: (a) Left: (b) Center:
(c) Right:
Option 2:
(2) Using
at top of shape, increasing downwards: (a) Left: (b) Center:
(c) Right:
Link to original
04
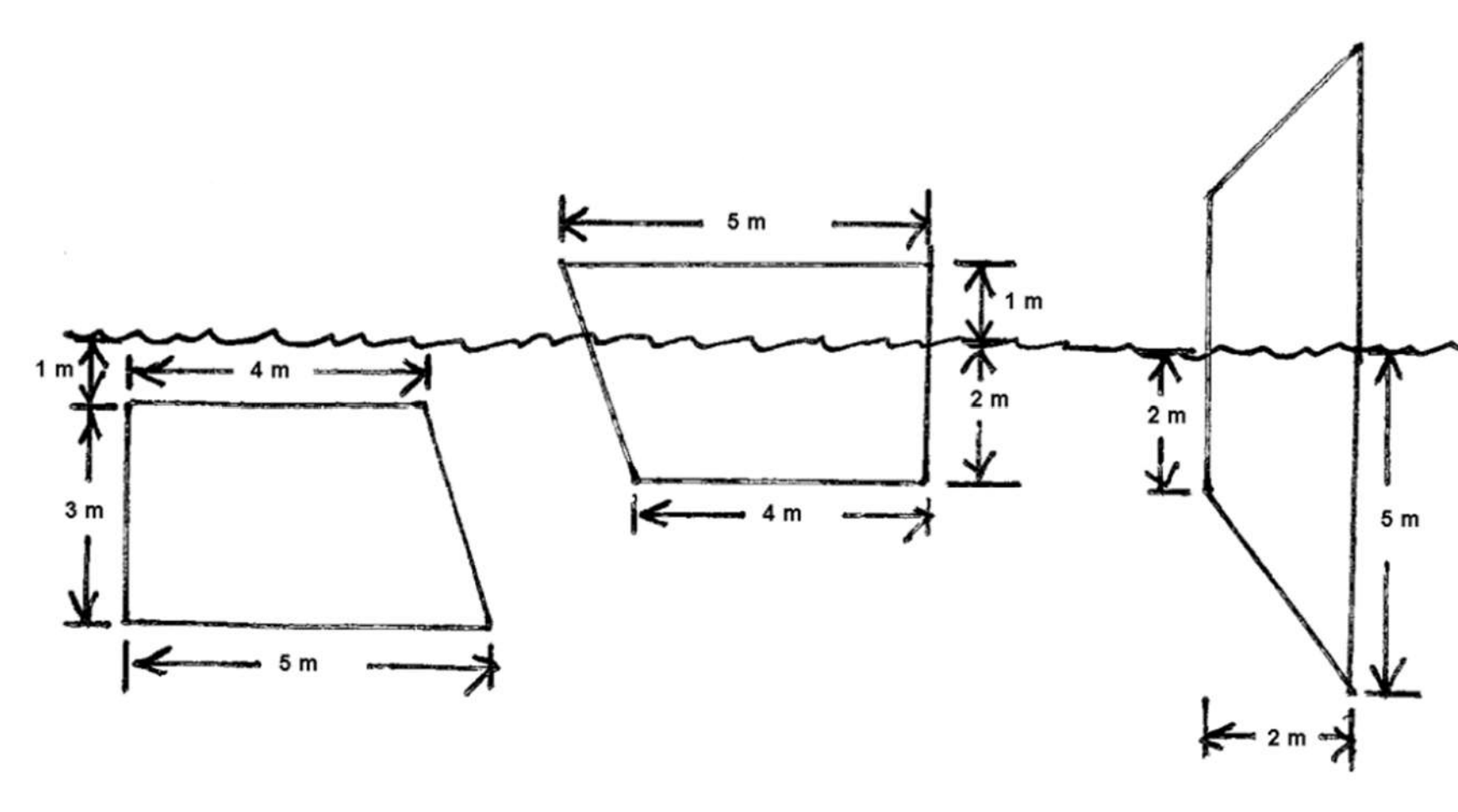
Fluid force on trapezoidal plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Link to originalSolution
02
(a) Left:
Set
at the water line, increasing downwards. Alternative: set
at the top of the trapezoid. Obtain:
(b) Center:
Set
at the water line, increasing downwards. Alternative: set
at the top of the trapezoid. Obtain:
(c) Right:
Set
at the water line, increasing downwards. Link to original
05
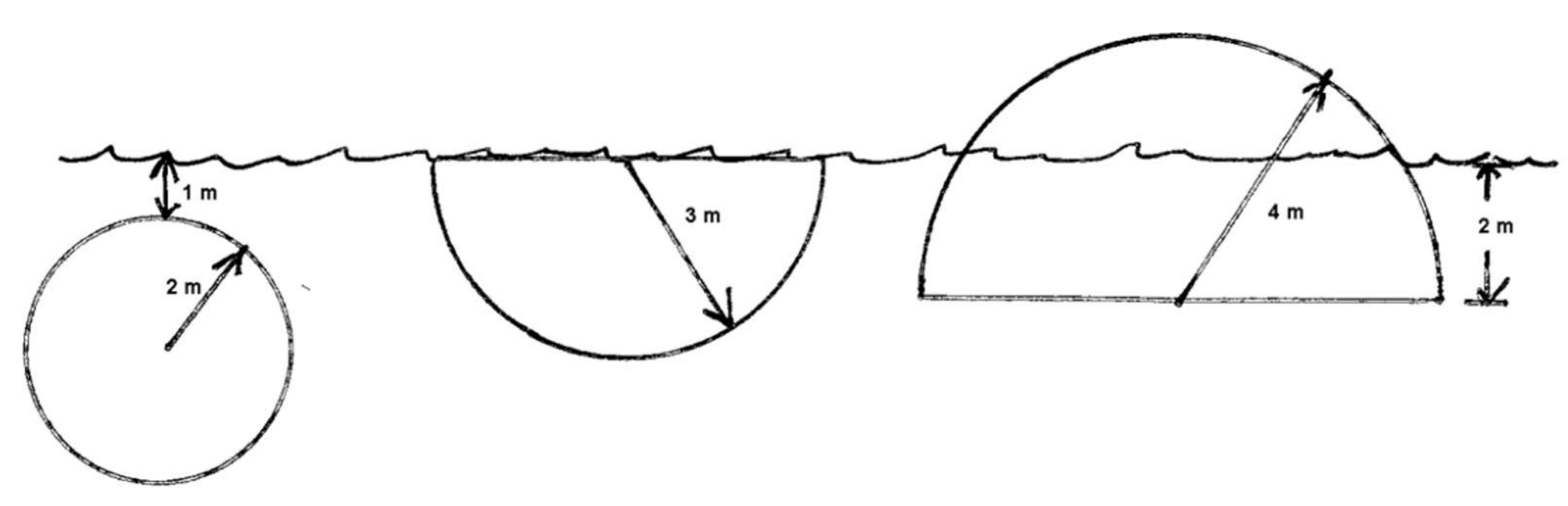
Fluid force on circular plates
For diagrams 1, 2, 3 (L to R) below, set up an integral to compute the hydrostatic force on the plate.
Link to originalSolution
07
(1) Integral formula:
Option 1:
(2) Using
at water line, increasing downwards: (a) Left: (b) Center:
(c) Right:
Option 2:
(2) Using
at center of shape, increasing downwards: (a) Left: (b) Center:
(c) Right:
Link to original
Moments and CoM
01
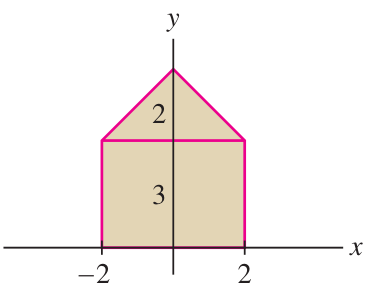
Center of mass of a house
A “house” is the region bounded by the (non-regular) pentagon with vertex points at
, , , , . Find the CoM of the house using additivity of moments.
Link to originalSolution
01
(1) Compute masses:
(2) Consider symmetries of rectangle:
Therefore
and: Therefore:
(3) Consider symmetry of triangle:
(4) Compute
by integration:
(5) Optional step: infer
:
(6) Additivity of moments:
(7) Compute CoM:
Thus:
Link to original
02
CoM of region between curves
Find the CoM of the region between the graph of
and the graph of over . Solution
02
Option 1: In terms of
. (1) Mass of region:
(2) Integral formula for
:
(3) Integral formula for
:
(4) Compute
:
Option 2: In terms of
. (1) Mass:
(2)
:
(3)
: Link to original
Work performed
01
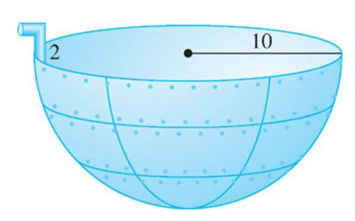
Pumping water from hemispherical tank
A hemispherical tank (radius
) is full of water. A pipe allows water to be pumped out, but requires pumping up above the top of the tank.
(a) Set up an integral that expresses the total work required to pump all the water out of the tank, assuming it is completely full.
(b) Now assume the tank start out full just to
. What does the integral become? Solution
03
(a) (1) Integral formula:
(2) Setup:
Coordinate system: set
at the top of the tank, increasing downwards. Horizontal slice of the tank: disk of radius
at depth , satisfies: Distance pumped up (add
for the spigot): Thus:
(b) (1) Change upper bound, top of water at
: Link to original
02
Building a conical tower
Set up an integral that expresses the work done (against gravity) to build a circular cone-shaped tower of height
and base radius out of a material with mass density . Solution
04
(1) Integral formula:
Option 1: (2) Setup:
Set
at the bottom, increasing upwards. Radius of the cone with a QLIF:
Horizontal slice of the cone tower: disk of radius
at height , satisfies: The slice at
is raised a distance of . Thus:
Option 2: (2) Setup:
Set
at the top of the cone, increasing downwards. Now
is the distance from the ground up to the height of a slice indexed by . Radius function:
Thus:
Link to original
03
Work to raise a leaky bucket
A bucket of water is raised by a chain to the top of a
-foot building. The water is leaking out, and the chain is getting lighter. The bucket weighs
, the initial water weighs , and the chain weighs , and the water is leaking at a rate of as the bucket is lifted at a constant rate of . What is the total work required to raise the bucket of water?
Link to originalSolution
08
(1) Integral formula:
Let
at the ground and increase going up.
(2) Compute force:
The force on the rope (at the top) when the bucket is at height
is: We know
. Water is leaking at
. Therefore: The weight of chain remaining is:
Put together:
(3) Integrate:
Link to original
Improper integrals
01
Comparison test
Use the comparison test to determine whether the integral converges:
Solution
03
(1) Find comparable integrand:
Higher power dominates for large
: Therefore, compare to
.
(2) Make comparison:
And:
because it is a
-integral with . By the Comparison Test, we conclude that:
Link to original
05
Computing improper integrals
For each integral below, give the limit interpretation of improper integral and then compute the limit. Based on that result, state whether the integral converges. If it converges, what is its value?
(a)
(b) (c) Solution
10
(a)
(1) Definition of improper integral:
(2) Antiderivative and limit:
Note A: Use L’Hopital:
(b)
(1) Definition of improper integral:
(2) Antiderivative and limit:
(c)
(1) Definition of improper integral:
(2) Antiderivative and limit:
Link to original