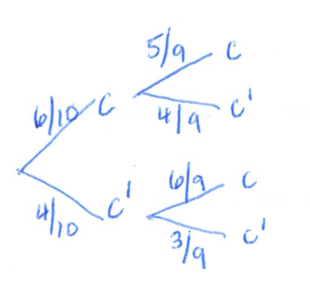Due date: Thursday 9/11, 11:59pm
Conditional probability
01
04
Multiplication - drawing two hearts
Two cards are drawn from a standard deck (without replacement).
(a) What is the probability that both are hearts?
(b) What is the probability that both are 4?
Link to originalSolution
16
(a)
Let
be the outcome of the first card, be the outcome of the second card, and denote “hearts”. Since there are 52 cards in a standard deck with 13 of them being hearts, we have (b)
Similarly to part (a), we have
Link to original
Bayes’ Theorem
02
02
Bayes’ Theorem - Inferring die from roll
A bag contains one 4-sided die, one 6-sided die, and one 12-sided die. You draw a random die from the bag, roll it, and get a 4.
What is the probability that you drew the 6-sided die?
Link to originalSolution
05
(1) Define events.
Let
be the event in which you draw the 4-sided die, be the event in which you draw the 6-sided die, and be the event in which you draw the 12-sided die. We are asked to compute
.
(2) Define obvious probabilities.
.
.
.
.
(3) Use Bayes’ Theorem to set up the formula for
.
(4) Plug in values and solve.
Link to original
Independence
03
04
Syntax errors vs. logic errors B
A computer program may contain a syntax error or a logic error or both types of errors. The probability that a program has both types of error is 0.16. The probability that a program has a syntax error given that it has a logic error is 0.4. The probability that a program has a logic error given that it has a syntax error is 0.5.
Are the events “program has a syntax error” and “program has a logic error” independent? Justify your answer.
Link to originalSolution
Tree diagrams
04
02
Homework part errors
A homework problem has 10 different parts. You submit and are told that 4 of the 10 answers you provided are incorrect, but you are not told which parts are incorrect.
(a) What is the probability you will have gotten the first part correct and the second part incorrect? Draw a tree diagram.
(b) Suppose the 4 errors have occurred in the first 6 parts. In this case, how many possible arrangements are there for these 4 errors?
(c) What is the probability the 4 errors occurred in the first 6 parts?
Link to originalSolution
18
(a)
Note:
gives the wrong answer! (b)
(c)
Link to original
Counting
05
09
Counting passwords
Suppose a password must be created using 5 letters and 6 digits. (There are 26 letters, a-z, and 10 digits, 0-9.) No letter or digit may be repeated.
(a) How many unique passwords can be created if the letters must come first and the digits last?
(b) How many unique passwords can be created if the 5 letters and 6 digits can appear in any order?
Link to originalSolution
13
(a)
(b)
Link to original
06
03
Drawing balls of distinct color
A bin contains 3 green and 4 yellow balls. Two balls are drawn out.
What is the probability that they are different colors?
Link to originalSolution
12
(1) Define relevant events.
If two balls of different colors are drawn out, then we choose one of each color.
Since order doesn’t matter, our sample space consists of all the ways we choose 2 balls out of 7.
(2) Compute probability.
Link to original
07
02
Wisconsin flag 2 of 3 days
A kindergarten class hangs a random state flag (50 flags) on the wall every day. What is the probability that two days out of three given days have Wisconsin’s flag?
Link to originalSolution
11
(1) Consider how the days are chosen.
Since we just want two days out three given days, it is unordered, so we account for this with the
term.
(2) Consider the probability that Wisconsin’s flag is hung on the first two days, and not the third.
The probability that Wisconsin’s flag is hung up is
, and the probability it’s any other flag is . Therefore, the desired probability is
.
(3) Combine terms.
Link to original
Review problems
08
03
Inclusion-exclusion reasoning
Suppose
and . Show that . Link to originalSolution
17
(1) State the inclusion-exclusion principle.
(2) Examine the maximum value of
. We know that
. Given that
and , .
(3) Examine the minimum value of
. The minimum value of
is the maximum of the individual values.
. Therefore,
Link to original.