Due date: Sunday 2/1, 11:59pm
Partial fractions
01
04
Link to originalPartial fractions - irreducible quadratic
Compute the integral:
Solution
Solutions - 0060-04
(1) Perform long division:
(2) Use
to integrate: Recall formula:
Choose
. Then: The final answer is therefore:
Link to original
02
05
Link to originalPartial fractions - long division
Compute the integral:
Solution
Solutions - 0060-05
(1) Numerator degree is not smaller! Long division first:
(2) Factor denominator:
(3) Write the partial fractions general form equation (for the second term):
(4) Solve for constants:
Cross multiply:
Plug in
, obtain so . Plug in
, obtain so .
(5) Integrate by terms:
Link to original
03
06
Link to originalPartial fractions - big generic
Give the generic partial fraction decomposition (no need to solve for the constants):
Solution
Solutions - 0060-06
(1) Observe that
: On the other hand,
cannot be factored further. (Its zeros are imaginary.) Now all denominator factors are either linear or irreducible quadratic.
(2) Write the partial fractions general form equation:
(3) Notice a few things:
Link to original
- Quadratic
acquires linear term on top - Linear
is to 3rd power so it has repetition up to 3rd power - Linear
and are only to 1st power.
04
07
Link to originalPartial fractions - linear and quadratic
Compute the integral:
Solution
Solutions - 0060-07
(1) Denominator has degree 3, numerator has degree 2, therefore long division is not necessary.
(2) Write the partial fractions general form equation:
Notice that
is an irreducible quadratic (cannot be factored). So we have:
(3) Solve for constants:
Cross multiply:
Plug in
, obtain: Expand RHS:
Comparing
terms, obtain: and thus . Comparing constant terms,
.
(4) Integrate by terms:
Note A: For the last term, use the formula:
Link to original
05
08
Link to originalPartial fractions - repeated factor
Compute the integral:
Solution
Solutions - 0060-08
(1) Write the partial fractions general form equation:
Observe that
appears in degree 3 in the integrand, so we have one term for each power up to 3 in the partial fraction decomposition.
(2) Solve for constants:
Cross multiply:
Plug in
, obtain so . Plug in
, obtain . Plug in
, obtain: Plug in
, obtain:
(3) Integrate each term:
Optional simplification:
Link to original
06
09
Link to originalPartial fractions - rationalize first
For each of these integrals, make a
-substitution that changes the integrand into a rational function. Write the integral in terms of for your answer. You do not have to compute the -integral. (a)
(b)
Solution
Solutions - 0060-09
(a) (1)
-substitution with and : Notice that
. Then:
(2) Partial fractions:
Therefore:
(b) (1) Set
:
(2) Partial fractions:
Therefore:
Link to original
Simpson’s Rule
07
02
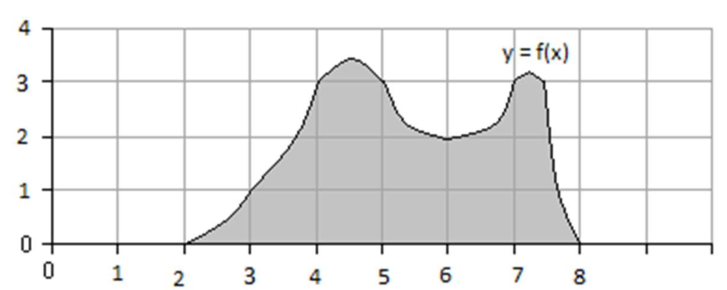
Link to originalSimpson’s Rule for volume by shells
Use Simpson’s Rule with
to compute the volume of the solid obtained by revolving the pictured region about the -axis. Can you do it without using a calculator?
Solution
Solutions - 0070-02
(1) Recall shells formula:
(2) Interpret:
Bounded above by
. Bounded below by -axis. Bounded left by
. Bounded right by . Obtain:
(3) Create table of values to apply Simpson’s Rule:
(4) Recall Simpson’s Rule formula:
Here
since in this formula represents the integrand values. Note that
. Plug in:
Therefore:
Therefore:
Link to original
08
03
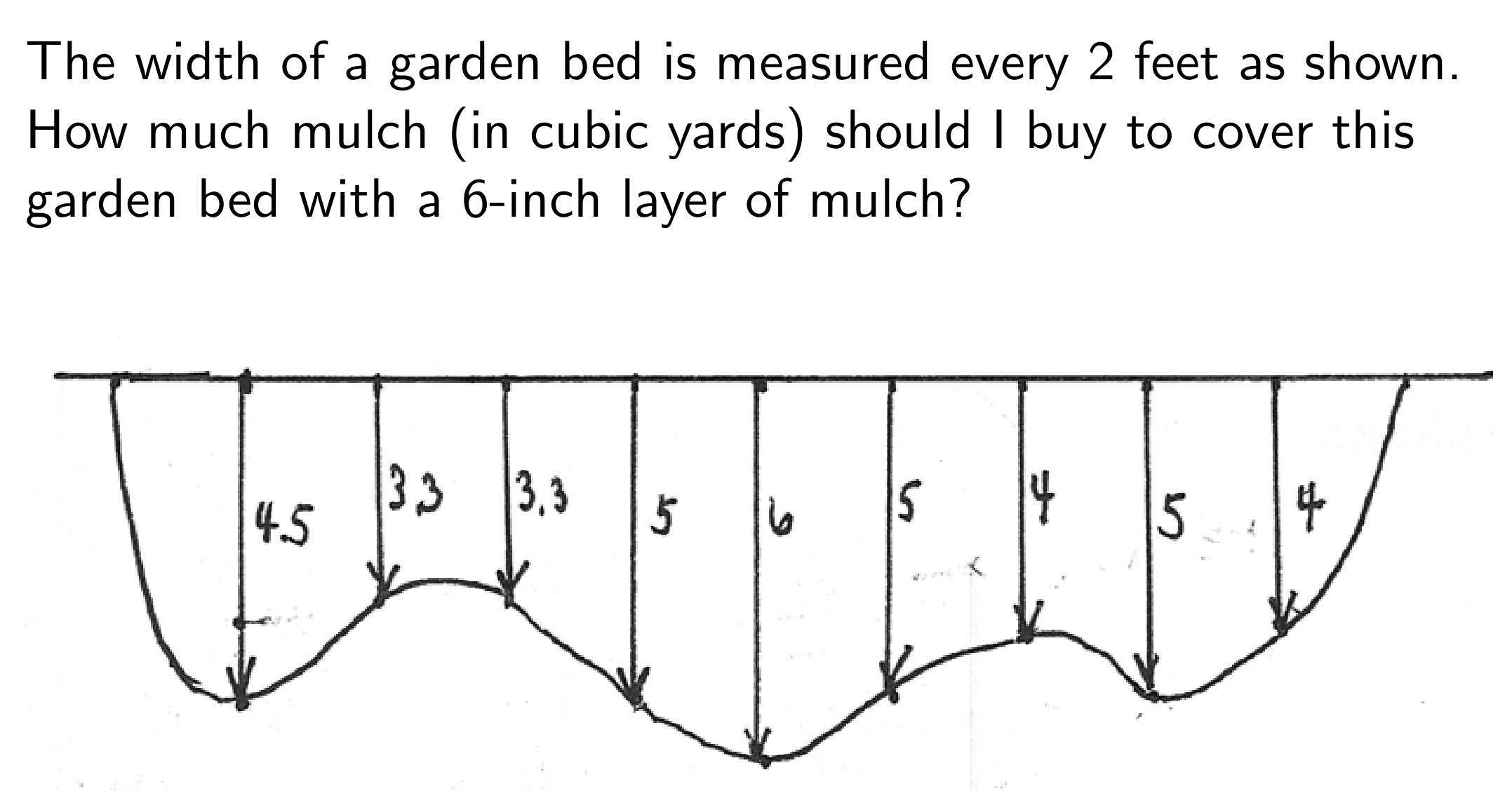
Link to originalArea of a garden bed
Solution
Solutions - 0070-03
Note: you can also start from
and . This gives a different answer, . (1) Set up integration:
Set
at the left upper corner, with extending to the right, extending downwards. Then:
(2) Create table of values:
(3) Recall Simpson’s Rule formula:
Here
and . Thus:
(4) Compute cubic yards from known surface area:
Mulch is
deep, so the volume is: Link to original