Stepwise problems - Thu. 11:59pm
Moments and CoM
01
01
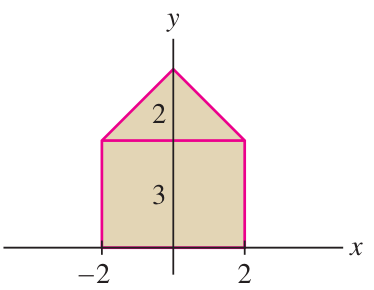
Link to originalCenter of mass of a house
A “house” is the region bounded by the (non-regular) pentagon with vertex points at
, , , , . Find the CoM of the house using additivity of moments.
Solution
02
02
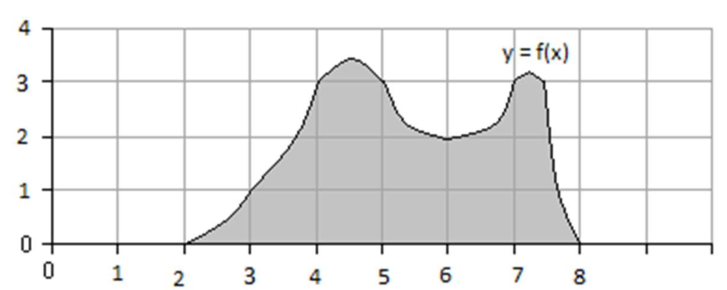
Link to originalCoM of region between curves
Find the CoM of the region between the graph of
and the graph of over .
Solution
Improper integrals
03
01
Link to originalComparison test
Use the comparison test to determine whether the integral converges:
Solution
Regular problems - Sun. 11:59pm
Moments and CoM
04
03
Link to originalFlatCoMMan
Find the center of mass of FlatCoMMan. Assume a constant mass density
. Use additivity of moments.
Solution
05
04
Link to originalCoM from Simpson’s
Use Simpson’s rule (with 6 subintervals) to estimate the centroid of this region:
You will need to estimate
and and with three separate integrals. You can use a calculator for your arithmetic.
Solution
Improper integrals
06
02
Link to originalProper vs. improper
For each integral below, determine whether it is proper or improper, and if improper, explain why.
(a)
(b) (c) (d)
(e) (f)
Solution
07
03
Link to originalGabriel’s Horn - Volume and surface of revolution
The curve
for is rotated about the -axis. The resulting shape is Gabriel’s Horn. (a) Find the volume enclosed by the horn by evaluating a convergent improper integral.
(b) Show that the surface area of the horn is infinite by applying comparison to a
-integral which is divergent.
Solution
08
04
Link to originalComputing improper integrals
For each integral below, give the limit interpretation of improper integral and then compute the limit. Based on that result, state whether the integral converges. If it converges, what is its value?
(a)
(b) (c)
Solution
09
05
Link to originalComputing improper integrals
For each integral below, give the limit interpretation of improper integral and then compute the limit. Based on that result, state whether the integral converges. If it converges, what is its value?
(a)
(b) (c)
Solution