W07 - Notes

Sequences

Videos

Review Videos

Videos, Math Dr. Bob:

• Infinite sequences: Definition; Squeeze Theorem
  • Extra: Infinite sequences: Various examples, arithmetic and geometric
  • Extra: Infinite sequences: Recursive sequences (like Fibonacci)

Link to original

01 Theory

Theory 1

A sequence is a rule that defines a term for each natural number :

So a sequence is a function from to .

Geometric sequence

A sequence is called geometric if the ratio of consecutive terms is some constant , independent of :

The defining relation of a geometric sequence is equivalent to .

By plugging into , we have . This plugging can be repeated -times to get a formula for the term:

Therefore , and we have a formula for the general term of the sequence (the term with index ).

Starting point of a sequence

Note that sometimes the index (variable) of a sequence starts somewhere other than . Most common is but any other starting point is allowed, even negative numbers.

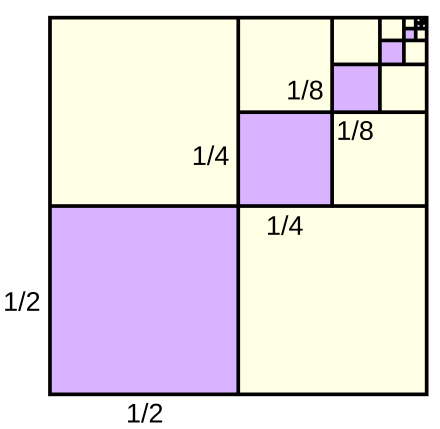
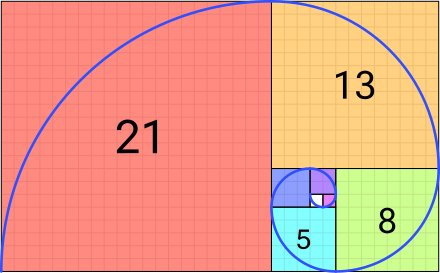
Sometimes is used instead of in the formula for the general term of a sequence, thus . The ‘’ notation is useful when the sequence starts from .

Extra - Fibonacci sequence

The Fibonacci sequence goes like this:

The pattern is:

This formula is a recursion relation, which means that terms are defined using the values of prior terms.

The Fibonacci sequence is perhaps the most famous sequence of all time. It is related to the Golden Ratio and the Golden Spiral:

Link to original

02 Illustration

Example: Geometric sequence - revealing the format

Geometric sequence: revealing the format

Find and and (written in the geometric sequence format) for the following geometric sequences:

(a) (b)
(c)

Solution

(a) Plug in to obtain . Notice that and so therefore . Then the ‘general term’ is .

---

(b) Rewrite the fraction:

Plug that in and observe . From this format we can read off and .

---

(c) Rewrite:

From this format we can read off and .

Link to original

Series

Videos

Review Videos

Videos, Math Dr. Bob:

• Infinite series: Definitions, basic examples
• Geometric series and SDT: Geometric series, Simple Divergence Test (aka “Limit Test”)
• Infinite series: Various examples
  • Extra: Infinite series convergence: Telescoping series

Link to original

03 Theory

Theory 1

A series is an infinite sum that is created by successive additions without end. The terms are not added up “all at once” but rather they are added up “as increases” or “as .”

Three of the most famous series are the Leibniz series and the geometric series:

---

Partial sum sequence of a series

The partial sum sequence of a series is the sequence whose terms are the sums up to the given index:

These terms themselves form a sequence:

Link to original

04 Illustration

Example: Geometric series - total sum and partial sums

Geometric series - total sum and partial sums

The geometric series total sum can be calculated using a “shift technique” as follows: (1) Compare and :

(2) Subtract second line from first line, many cancellations:

(3) Solve to find :

Note: this calculation assumes that exists, i.e. that the series converges.

The geometric series partial sums can be calculated similarly, as follows:

(1) Compare and :

(2) Subtract second line from first line, many cancellations:

(3) Solve to find :

(4) The last formula is revealing in its own way. Here is what it means in terms of terms:

Link to original

Convergence

Videos

Review Videos

Videos, Math Dr. Bob:

• Infinite sequences convergence: Squeeze; Monotone Bounded
• Infinite sequences convergence: Examples sequences: convergent, monotonic, bounded

Link to original

05 Theory

Theory 1

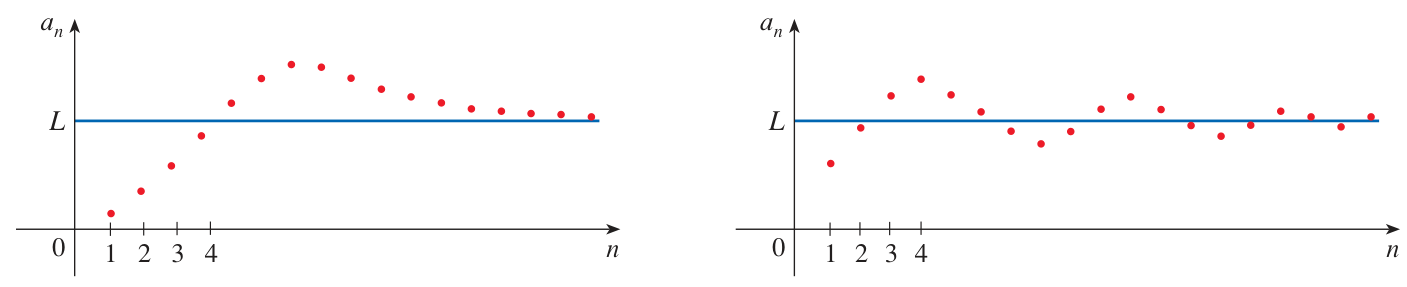
A sequence has a limit if its terms tend toward a specific number, or toward .

When this happens we can write “” with some number or . We can also write “ as ”.

The sequence is said to converge if it has a finite limit .

Some sequences don’t have a limit at all, like :

Or :

These sequences diverge. In the second case, there is a limit , so we say it diverges to .

A sequence may have a limit of but is still said to diverge.

Extra - Convergence definition

The precise meaning of convergence is this. We have as if, given any proposed error , it is possible to find such that for all we have .

When , convergence means that given any , we can find such that for all we have .

Similarly for .

---

If the general term is a continuous function of , we can replace with the continuous variable and compute the continuous limit instead:

If would be a differentiable function, and we discover an indeterminate form, then we can apply L’Hopital’s Rule to find the limit value. For example, if the indeterminate form is , we can convert it to and apply L’Hopital.

Link to original

06 Illustration

Example - L’Hopital’s Rule for sequence limits

L’Hopital’s Rule for sequence limits

(a) What is the limit of ? (b) What is the limit of ? (c) What is the limit of ?

Solution (a) Identify indeterminate form . Change from to and apply L’Hopital:

---

(b) Identify indeterminate form . Change from to and apply L’Hopital:

---

(c) (1) Identify form and rewrite as :

(2) Change from to and apply L’Hopital:

(3) Simplify:

(4) Consider the limit:

Link to original

Example - Squeeze theorem

Squeeze theorem

Use the squeeze theorem to show that as .

Solution

(1) We will squeeze the given general term above and below a sequence that we must devise:

(2) We need to satisfy and . Let us study .

(3) Now for the trick. Collect factors in the middle bunch:

(4) Each factor in the middle bunch is so the entire middle bunch is . Therefore:

Now we can easily see that as , so we set and we are done.

Link to original

07 Theory

Theory 2

Monotone sequences

A sequence is called monotone increasing if for every .

A sequence is called monotone decreasing if for every .

In this context, ‘monotone’ just means it preserves the increasing or decreasing modality for all terms.

Monotonicity Theorem

If a sequence is monotone increasing, and bounded above by , then it must converge to some limit , and .

If a sequence is monotone decreasing, and bounded below by , then it must converge to some limit , and .

Terminology:

• Bounded above by means that for every
• Bounded below by means that for every

Notice!

The Monotonicity Theorem says that a limit exists, but it does not provide the limit value.

Link to original

08 Illustration

Example - Monotonicity Theorem

Monotonicity

Show that converges.

Solution

(1) Observe that for all .

Because , we know .

Therefore

---

(2) Change to and show is decreasing.

New formula: considered as a differentiable function.

Take derivative to show decreasing.

Derivative of :

---

(3) Simplify:

Denominator is . Numerator is . So and is monotone decreasing.

Therefore is monotone decreasing as .

Link to original

09 Theory

Theory 3

Series convergence

We say that a series converges when its partial sum sequence converges:

Let us apply this to the geometric series. Recall our formula for the partial sums:

Rewrite this formula:

Now take the limit as :

So we see that converges exactly when . It converges to .

(If then the denominator is , and if then the factor does not converge.)

Furthermore, we have the limit value:

This result confirms the formula we derived for the total for a geometric series. This time we did not start by assuming exists, on the contrary we proved that exists. (Provided that .)

Extra - Aspects of and from the geometric series

Notice that we always have the rule:

This rule can be viewed as coming from partitioning the full series into a finite part and the remaining infinite part:

We can remove a factor from the infinite part:

The parenthetical expression is equal to , so we have the formula given above.

Link to original